IF-IG

Brought to you by

IF - IG

International Interdisciplinary Center For
Information and Fact Checking about
Info-Gap Decision Theory

Local time

Home	About	News	IGDT	The Campaign	Myths & Facts	Reviews	FAQs	FUQs	Resources	Contact Us
The rise and rise of voodoo decision making

Reviews of publications on Info-Gap decision theory (IGDT)

Review 9-2023 (Posted: June 27, 2023)

Reference Yang Liu, Melissa L. Thomas, Grey T. Coupland, Penghao Wang, Dan Zheng & Simon J. McKirdy Info‐gap theory to determine cost‐effective eradication of invasive species Scientific Reports 13: 2744.

Publication type Article

Year of publication 2023

Downloads .

Abstract Invasive species eradication campaigns often fail due to stochastic arrival events, unpredictable detectability and incorrect resource allocation. Severe uncertainty in model parameter estimates may skew the eradication policy results. Using info‐gap decision theory, this research aims to provide managers with a method to quantify their confidence in realizing successful eradication of particular invasive species within their specified eradication budgets (i.e. allowed eradication cost) in face of information‐gaps. The potential introduction of the Asian house gecko Hemidactylus frenatus to Barrow Island, Australia is used as a case study to illustrate the model. Results of this research demonstrate that, more robustness to uncertainty in the model parameters can be earnt by (1) increasing the allowed eradication cost (2) investment in pre‐border quarantine and border inspection (i.e. prevention) or (3) investment in post‐border detection surveillance. The combination of a post‐border spatial dispersal model and info‐gap decision theory demonstrates a novel and spatially efficient method for managers to evaluate the robustness of eradication policies for incursion of invasive species with unexpected behaviour. These methods can be used to provide insight into the success of management goals, in particular the eradication of invasive species on islands or in broader mainland areas. These insights will assist in avoiding eradication failure and wasteful budget allocation and labour investment.

Reviewer Moshe Sniedovich

IF-IG perspective This is a typical IGDT article in that, like many other articles on IGDT, it depicts a very distorted, unbalanced, often erroneous picture of the state of the art in decision-making under severe uncertainty and the role and place of IGDT in this field. It completely ignores well documented studies by Australian scholars that expose serious flaws in IGDT and its applications in applied ecology, as well as technical facts about IGDT that make it unsuitable for the treatment of severe uncertainty of the type it stipulates.

Ecologists and managers contemplating the use of IGDT should carefully consider its strengths and weaknesses, reviewed here, and not turn to it as a default approach in situations of severe uncertainty, irrespective of how this term is defined.

Hayes, Barry, Hosack and Peters (2013). Severe uncertainty and info-gap decision theory.
Methods in Ecology and Evolution, 4, 601–611.

The above is a quote from the most comprehensive survey of Ecological applications of IGDT to-date. Four areas of concern for IGDT in practice were identified in the survey, namely

Sensitivity to initial estimates,

Localised nature of the analysis,

Arbitrary error model parameterisation,

Ad hoc introduction of notions of plausibility.

Regarding the last concern, Hayes et al. (2013, p. 609) conclude the following:

Plausibility is being evoked within IGDT in an ad hoc manner, and it is incompatible with the theory's core premise, hence any subsequent claims about the wisdom of a particular analysis have no logical foundation. It is therefore difficult to see how they could survive significant scrutiny in real-world problems. In addition, cluttering the discussion of uncertainty analysis techniques with ad hoc methods should be resisted.

And in the article entitled "Robustness Metrics: How Are They Calculated, When Should They Be Used and Why Do They Give Different Results?" (McPhail et al. 2018, p.174) we read this explanation for why IGDT was not "considered further in this article":

Satisficing metrics can also be based on the idea of a radius of stability, which has made a recent resurgence under the label of info-gap decision theory (Ben-Haim, 2004; Herman et al., 2015). Here, one identifies the uncertainty horizon over which a given decision alternative performs satisfactorily. The uncertainty horizon α is the distance from a pre-specified reference scenario to the first scenario in which the pre-specified performance threshold is no longer met (Hall et al., 2012; Korteling et al., 2012). However, as these metrics are based on deviations from an expected future scenario, they only assess robustness locally and are therefore not suited to dealing with deep uncertainty (Maier et al., 2016). These metrics also assume that the uncertainty increases at the same rate for all uncertain factors when calculating the uncertainty horizon on a set of axes. Consequently, they are shown in parentheses in Table 2 and will not be considered further in this article.

In other words, IGDT was "considered further in this article" because its local orientation makes it unsuitable for the treatment of (deep) severe uncertainty. This feature of IGDT was known at least since 2003, was discussed in written technical reports since 2006 (e.g., Sniedovich 2006a, 2006b), and in peer-reviewed articles since 2007 (e.g., Sniedovich 2007).

And how about this assessment of IGDT (Johnson and Geldner (2019, p. 31)):

It does, however, have one major limitation: It considers only local uncertainty in the neighborhood of the best-estimate state of the world. Thus, it is most useful where a reasonable best estimate exists and there is strong reason to believe increasingly large deviations from the best estimate are decreasingly likely (Hayes et al. 2013). While this does not require the uncertainty to be well parameterized, it is a strong assumption nonetheless (Taleb 2005). If the future SOW is no more likely to be within an arbitrary neighborhood of the best estimate than far away from it, info-gap may lead to endorsement of strategies vulnerable to high regret.

Here as well, it is recognized that IGDT has a major limitation: the local orientation of its robustness analysis makes it unsuitable for the treatment of severe uncertainty.

For the benefit of readers who are not familiar with IGDT, and/or with this limitation of its robustness analysis, before we discuss the above comments, here is an informal explanation of what info-gap robustness is all about, how its deals with severe uncertainty, and why such a treatment is problematic.

What is IGDT's secrete weapon against severe uncertainty?

As a concept, "Info-gap robustness" is a reinvention of the well established (circa 1960) concept called Radius of Stability. It is a measure of local robustness defined as the distance from the nominal value of a parameter to the region of instability. In the context of IGDT, it is the distance from the point estimate of the uncertainty parameter to constraints violation. In pictures:

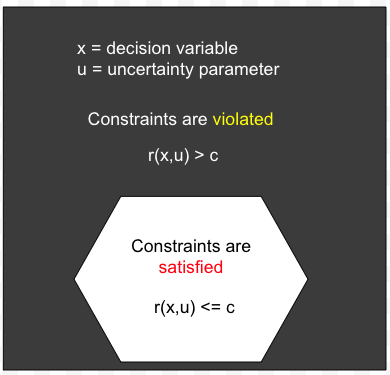
The uncertainty space is the set of all possible values of the uncertainty parameter $u$ under consideration. We don't know which value will be realized. IGDT allows the uncertainty space to be unbounded. It is often argued (erroneously!) that this feature of IGDT, namely its ability to deal with unbounded uncertainty, distinguishes it from other methods for the treatment of severe uncertainty, such as Wald's maximin paradigm.
For each value of the decision variable, the uncertainty space $U$ is partitioned into two part: one part consists of all the values of $u$ that satisfy the performance constraint $r(x,u) \le c$ (the set painted white), the other consists of all the value of $u$ that violates the constraint (the set painted black).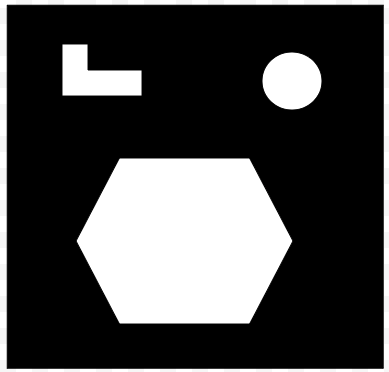

The above example is meant to emphasize the fact that IGDT does not impose any restrictions on the performance function $r$ other that it is a real-valued function of the decision variable $x$ and the uncertainty parameter $u$. Therefore, IGDT allows the partition of $U$ to be "strange", meaning that the theory must be general enough to cater for strange looking partitions.
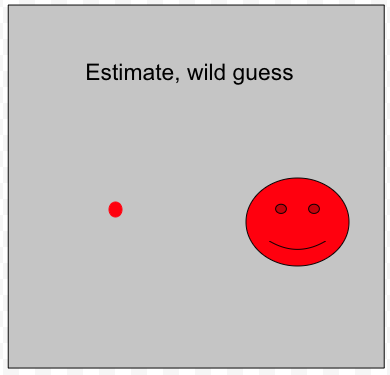
IGDT assumes that although the uncertainty is severe, we do have a point estimate of the true value of $u$. Needless to say, because the uncertainty is assumed to be severe, it is also assumed that the estimate is poor, can be substantially wrong, even just a "wild guess". Note that it is not assumed that the severely unknown true value of $u$ is more likely to be in the neighborhood of the estimate than in any other neighborhood in the uncertainty space. Indeed, IGDT prides itself for being probability-free, likelihood-free, chance-free, plausibility-free, belief-free, and so on.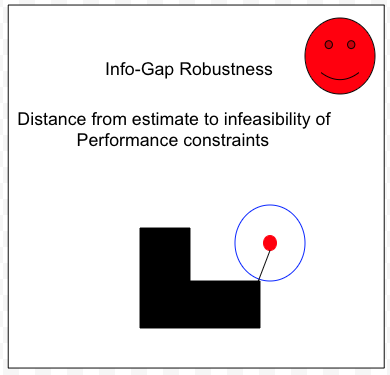

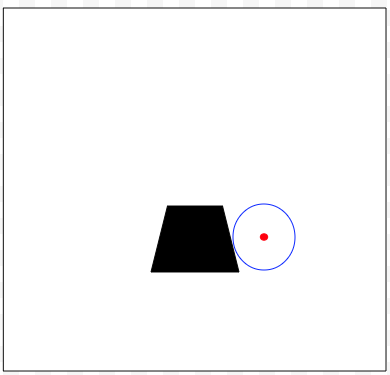
The above illustrates graphically the concept "info-gap robustness". Informally speaking, the info-gap robustness of a decision is the (shortest) distance from the estimate to violation of the constraints. As illustrated above, this distance is equal to the size (radius) of the largest neighborhood around the estimate over which the constraints are satisfied. Note that in this context a neighborhood is not necessarily a circle. The basic property of the neighborhoods in that are nested. The above is an illustration of a case where the decision is quite robust (large white area) but the info-gap robustness of the decision in question is relatively small because the estimate is close to an area of the uncertainty space where the decision violates the constraint (black area).

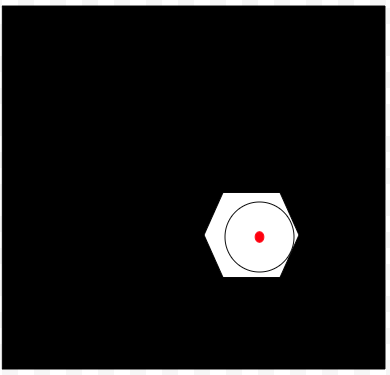
Another example of how info-gap robustness is determined. In this case the decision is not very robust (large black area). Here we begin to address an important issue that explains why IGDT is inherently a theory of local robustness and why it is not suitable for the treatment of severe uncertainty of the type that it was designed to handle. I call this issue "The No-man's Land" issue.
Suppose that $u'$ is located in the uncertainty space at a point whose distance from the estimate is larger that the info-gap robustness of the decision under consideration, call it $x'$, that is larger than the radius of the largest "safe" neighborhood around the estimate. Then, from the way "info-gap robustness" is defined, it follows that the value of the performance level $r(x',u')$ has no impact whatsoever on the robustness analysis of "x'". This means that all the values of $u$ outside the "safe" neighborhood, have no impact whatsoever on the robustness analysis, and the value assigned to the info-gap robustness of decision $x'$. In short, the info-gap robustness of decision $x'$ is independent of the values of $r(x',u)$ over the complement of the "safe" neighborhood associated with decision $x'$ and its border.

So, schematically speaking, the above picture tells us the following interesting story.

There is a theory called IGDT that claims to be able to handle severe uncertainty where

The uncertainty space can be unbounded,

The point estimate can be a wild guess,
The robustness of a decision is independent of the how well/badly the decision performs over a very large portion of the uncertainty space.

Needless to say, such a theory falls under the category Too good to be true!

Some IGDT scholars accuse me of exaggerating the importance of the "No Man's Land" issue, and its impact on IGDT's ability to adequately treat severe uncertainties of the type it was designed to handle. In particular, I was accused on deliberately exaggerating the size of the "safe neighborhood" around the estimate.

My answer is this: IGDT prides itself for being able to handle unbounded uncertainty spaces. In fact, Ben-Haim (2001, 2006, 2010) indicates that indeed quite often this is the case in practice.

It is therefore important to stress that in cases where the uncertainty space is unbounded and the problem is non-trivial, the size of the "safe neighborhood" is infinitesimally small (compared to the size of the uncertainty space). Therefore, it is perfectly legitimate to draw a very small white circle, as done above.

In short, the secret weapon that enables IGDT to handle extremely severe uncertainties, including cases where the uncertainty space is unbounded, is this:

IGDT's secret weapon against severe uncertainty Ignore the severity of the uncertainty, and the No-Man's Land" issue. Simply conduct a local Radius of Stability analysis (circa 1960) around the "wild guess".

I should point out that all of this was known at least since the end of 2003, was discussed in IGDT circles in Australia extensively since then, and was studied in peer-reviewed articles.

Some unavoidable questions

In view of the above, there are many questions regarding the assessment of IGDT as a tool for decision-making under severe uncertainty in Liu et al. (2023). In this review I focus on this:

An Unavoidable Question As seen above, there are strong indications that IGDT is unsuitable for the treatment of problems involving decision-making under severe uncertainty. How then the choice of IGDT for this purpose is justified in Liu et al. (2023)?

Liu et al. (2023, p. 2) explain that the ecological problem under consideration features severe (deep) uncertainty and justify the choice of IGDT as a proper tool for treating this problem as follows:

For situations facing deep uncertainty, info-gap decision theory (IGDT) has proven to be useful^15,16. This is the first application of IGDT to generate cost-effective, but also robust eradication policy to manage insular invasive species with limited budgets.

So let us take a look at references [15] and [16]. In [15. p. 290] we read:

The main contribution of this paper is to point the way toward a new way of dealing with severe uncertainty in the biological inspection realm that incorporates economic data and, as importantly, is free of the problems associated with risk assessment in a truly uncertain environment. The model developed in this paper incorporates economic aspects of inspection and inspection failure via the concept of robustness of choice over severely uncertain model elements. This same approach is applicable to an increasingly wide range of detection problems where uncertainty reigns and effective use of scarce inspection resources are required.

But there is no evidence and no explanation in [15] as to what makes IGDT capable of dealing properly with severe uncertainty.

In [16, p. 840] we read this:

Info-gap decision theory is very useful when uncertainty is so severe that it is difficult to obtain probability distributions of parameters. Info-gap decision theory has been applied to decisions in conservation (Regan et al. 2005; McDonald-Madden et al. 2008), design of marine protected areas (Halpern et al. 2006), and forest management (McCarthy and Lindenmayer 2007) among other areas of environmental sciences (Ben-Haim 2006).

But there is no evidence and no explanation in [16] as to what makes IGDT actually capable of dealing properly with severe uncertainty.

Interestingly, regarding the reference in [16] to McCarthy and Lindenmayer (2007), it turns out that McCarthy had a change of heart about IGDT suitability for the treatment of severe uncertainty. In McCarthy (2013, p. 87-88) we read:

While use of info-gap decision theory has increased, so have criticisms. I have published papers using info-gap decision theory,^71-74 but now I agree with critics that it over- states the level of uncertainty that it accommodates. Sniedovich^75-78 is a vocal critic, although some turns of phrase (e.g., referring to "voodoo decision making") and his mathematical treatment might obscure the case in the eyes of many ecologists. Simultaneously, Sniedovich⁷⁸ argues that defenders of info-gap do not address his major criticisms, which essentially dispute the form of uncertainty analyzed by info-gap decision theory⁷⁰.

So it looks like McCarthy is also an IGDT skeptic now!

Regarding my use of the term "voodoo decision making", I should stress that I use it when ... it is appropriate to use it, for example, in discussions about the flaws in IGDT.

Taking into account the discussion above, we reach

An Unavoidable Conclusion No. 1
The inherently local orientation of IGDT's robustness analysis makes IGDT unsuitable for the treatment of severe uncertainty. In fact, the more severe the uncertainty the more problematic is the use of IGDT.

Therefore, there is no reason to believe that IGDT is a suitable tool for the treatment of the severe (deep) uncertainty postulated in Liu et al. (2023). Not only that Liu et al. (2023) do not provide evidence that the choice of IGDT is justified, the article ignores the conclusions in peer reviewed articles explaining why IGDT is unsuitable for the treatment of severe uncertainty.

Liu et al. (2023) also ignore formal rigorous proofs that IGDT's robustness model and robust-satisficing decision models are in fact Wald-type maximin models, hence the following statement in Liu et al. (2023, p. 2) is non-sensical:

While under Knightian uncertainty eluding distribution specification, Wald’s maximin is a common method to deal with uncertainty by minimizing worst outcome. Alternatively, IGDT offers a method to quantify the confidence in realising specified aspirations and enable the balance between them²¹.

Being itself a maximin theory, IGDT cannot possibly be an alternative to ... the maximin paradigm! Do Liu et al. (2023) suggest that IGDT's two core models are not maximin models? If so, where is the proof?

Remark. I raised this very important Maximin/IGDT issue in Review 6, about 10 months before Liu et al. (2023) was submitted for publication! Go figure.

An Unavoidable Conclusion No. 2
Where were the referees of this article?

One expects a peer-reviewed article to provide a balanced assessment of the suitability of the method/theory used in the article to address the problem/issue/question under consideration. It seems that the referees of Liu et al. (2023) are not sufficiently familiar with the literature on IGDT.

This is not Breaking News. It happens very often. And this is the reason, dear reader, that I decided to "selectively review" IGDT publications on my site.

A more formal analysis of the reasons why IGDT is not suitable for the the treatment of severe (deep) uncertainty can be found in Review 2.

Summary and conclusions

In this review I continue my effort to fact-check publications about IGDT. Unfortunately, the need for this type of fact-checking is still needed because publications about IGDT, such as peer-reviewed articles and books, are not properly reviewed.

Given the obvious limitations of IGDT as far as the treatment of severe uncertainty is concerned, it is not clear why peer-reviewed journals continue to publish articles claiming, or arguing, that IGDT is a suitable tool for the treatment of severe uncertainty, without demanding the authors to justify this claim, and deal properly with well established counter-claims.

Liu et al. (2023) is a recent example of such a paper, and so is its predecessor that I reviewed here in January 2022.

Bibliography

C. McPhail , H. R. Maier , J. H. Kwakkel , M. Giuliani , A. Castelletti , and S. Westra (2018). Robustness metrics: how are they calculated, when should they be used and why do they give different results?Earth's Future 6:169-19.

Cameron McPhail (2020). Towards a better understanding of scenarios and robustness for the long-term planning of water and environmental systems. PHD thesis, The University of Adelaide, Australia.

Michael McCarthy (2014). Contending with uncertainty in conservation management decisions. Annals of the New York Academy of Sciences1322:77-91.

Sniedovich, (2006). What’s Wrong with Info-Gap? An Operations Research Perspective. Working Paper No. MS-1-06, Department of Mathematics and Statistics, The university of Melbourne.

Sniedovich (2006). Eureka! Info-Gap is Worst Case (maximin) in Disguise! Working Paper No. MS-2-06, Department of Mathematics and Statistics, The University of Melbourne.

Sniedovich, M. (2007). The Art and Science of Modeling Decision-Making Under Severe Uncertainty. Journal of Decision Making in Manufacturing and Services 1(1-2):111-136.

Sniedovich, M. (2008). Wald's Maximin Model: A Treasure in Disguise! Journal of Risk Finance 9(3):278-291.

Sniedovich, M. (2010). A bird’s view of info-gap decision theoryThe Journal of Risk Finance.11(3):268-283.

Sniedovich, M. (2012). Black swans, new Nostradamuses, voodoo decision theories and the science of decision-making in the face of severe uncertainty, International Transactions in Operations Research 19(1-2), 253-281.

Sniedovich, M. (2011). Info-gap decision theory: a perspective from the land of the Black Swan. Working Technical Report SM-01-11, Department of Mathematics and Statistics, The University of Melbourne.

Sniedovich, M. (2014). The elephant in the rhetoric on info-gap decision theory. Ecological Applications 24(1):229-233.

Sniedovich, M. (2014). Response to Burgman and Regan: The elephant in the rhetoric on info-gap decision theory. Ecological Applications 24(1):229-233.

Sniedovich, M. (2016). Wald's mighty maximin: a tutorial. International Transactions in Operational Research 23(4):625-653.
Sniedovich, M.(2016) From statistical decision theory to robust optimization: a maximin perspective on robust decision-making. In Doumpos, M., Zopounidis, C., and Grigoroudis, E. (eds.) Robustness Analysis in Decision Aiding, Optimization, and Analytics, pp. 59-87. Springer, New York.

Keith R. Hayes, Simon C. Barry, Geoffrey R. Hosack and Gareth W. Peters (2013). Severe uncertainty and info-gap decision theory. Methods in Ecology and Evolution 4:601-611.

Yang Liu, Penghao Wang, Melissa L. Thomas, Dan Zheng & Simon J. McKirdy (2021). Cost‐effective surveillance of invasive species using info‐gap theory. Scientific Reports 11:22828.

David R. Johnson and Nathan B. Geldner (2019). Annual Reviews of Resource Economics 11:19-41.

Relevant Links

An Info-Gap directory. Plenty of resources, including articles and lectures.

Review 2, 2022. A comprehensive review of IGDT.

Review 6, 2022. Review of a similar article.

Review 8, 2023. A detailed proof that the two core models of IGDT are maximin models.

Reference	Yang Liu, Melissa L. Thomas, Grey T. Coupland, Penghao Wang, Dan Zheng & Simon J. McKirdy Info‐gap theory to determine cost‐effective eradication of invasive species Scientific Reports 13: 2744.
Publication type	Article
Year of publication	2023
Downloads	.
Abstract	Invasive species eradication campaigns often fail due to stochastic arrival events, unpredictable detectability and incorrect resource allocation. Severe uncertainty in model parameter estimates may skew the eradication policy results. Using info‐gap decision theory, this research aims to provide managers with a method to quantify their confidence in realizing successful eradication of particular invasive species within their specified eradication budgets (i.e. allowed eradication cost) in face of information‐gaps. The potential introduction of the Asian house gecko Hemidactylus frenatus to Barrow Island, Australia is used as a case study to illustrate the model. Results of this research demonstrate that, more robustness to uncertainty in the model parameters can be earnt by (1) increasing the allowed eradication cost (2) investment in pre‐border quarantine and border inspection (i.e. prevention) or (3) investment in post‐border detection surveillance. The combination of a post‐border spatial dispersal model and info‐gap decision theory demonstrates a novel and spatially efficient method for managers to evaluate the robustness of eradication policies for incursion of invasive species with unexpected behaviour. These methods can be used to provide insight into the success of management goals, in particular the eradication of invasive species on islands or in broader mainland areas. These insights will assist in avoiding eradication failure and wasteful budget allocation and labour investment.
Reviewer	Moshe Sniedovich
IF-IG perspective	This is a typical IGDT article in that, like many other articles on IGDT, it depicts a very distorted, unbalanced, often erroneous picture of the state of the art in decision-making under severe uncertainty and the role and place of IGDT in this field. It completely ignores well documented studies by Australian scholars that expose serious flaws in IGDT and its applications in applied ecology, as well as technical facts about IGDT that make it unsuitable for the treatment of severe uncertainty of the type it stipulates.


The uncertainty space is the set of all possible values of the uncertainty parameter $u$ under consideration. We don't know which value will be realized. IGDT allows the uncertainty space to be unbounded. It is often argued (erroneously!) that this feature of IGDT, namely its ability to deal with unbounded uncertainty, distinguishes it from other methods for the treatment of severe uncertainty, such as Wald's maximin paradigm.		For each value of the decision variable, the uncertainty space $U$ is partitioned into two part: one part consists of all the values of $u$ that satisfy the performance constraint $r(x,u) \le c$ (the set painted white), the other consists of all the value of $u$ that violates the constraint (the set painted black).


The above example is meant to emphasize the fact that IGDT does not impose any restrictions on the performance function $r$ other that it is a real-valued function of the decision variable $x$ and the uncertainty parameter $u$. Therefore, IGDT allows the partition of $U$ to be "strange", meaning that the theory must be general enough to cater for strange looking partitions.		IGDT assumes that although the uncertainty is severe, we do have a point estimate of the true value of $u$. Needless to say, because the uncertainty is assumed to be severe, it is also assumed that the estimate is poor, can be substantially wrong, even just a "wild guess". Note that it is not assumed that the severely unknown true value of $u$ is more likely to be in the neighborhood of the estimate than in any other neighborhood in the uncertainty space. Indeed, IGDT prides itself for being probability-free, likelihood-free, chance-free, plausibility-free, belief-free, and so on.


The above illustrates graphically the concept "info-gap robustness". Informally speaking, the info-gap robustness of a decision is the (shortest) distance from the estimate to violation of the constraints. As illustrated above, this distance is equal to the size (radius) of the largest neighborhood around the estimate over which the constraints are satisfied. Note that in this context a neighborhood is not necessarily a circle. The basic property of the neighborhoods in that are nested.		The above is an illustration of a case where the decision is quite robust (large white area) but the info-gap robustness of the decision in question is relatively small because the estimate is close to an area of the uncertainty space where the decision violates the constraint (black area).


Another example of how info-gap robustness is determined. In this case the decision is not very robust (large black area).		Here we begin to address an important issue that explains why IGDT is inherently a theory of local robustness and why it is not suitable for the treatment of severe uncertainty of the type that it was designed to handle. I call this issue "The No-man's Land" issue. Suppose that $u'$ is located in the uncertainty space at a point whose distance from the estimate is larger that the info-gap robustness of the decision under consideration, call it $x'$, that is larger than the radius of the largest "safe" neighborhood around the estimate. Then, from the way "info-gap robustness" is defined, it follows that the value of the performance level $r(x',u')$ has no impact whatsoever on the robustness analysis of "x'". This means that all the values of $u$ outside the "safe" neighborhood, have no impact whatsoever on the robustness analysis, and the value assigned to the info-gap robustness of decision $x'$. In short, the info-gap robustness of decision $x'$ is independent of the values of $r(x',u)$ over the complement of the "safe" neighborhood associated with decision $x'$ and its border.


So, schematically speaking, the above picture tells us the following interesting story. There is a theory called IGDT that claims to be able to handle severe uncertainty where The uncertainty space can be unbounded, The point estimate can be a wild guess, The robustness of a decision is independent of the how well/badly the decision performs over a very large portion of the uncertainty space. Needless to say, such a theory falls under the category Too good to be true!		Some IGDT scholars accuse me of exaggerating the importance of the "No Man's Land" issue, and its impact on IGDT's ability to adequately treat severe uncertainties of the type it was designed to handle. In particular, I was accused on deliberately exaggerating the size of the "safe neighborhood" around the estimate. My answer is this: IGDT prides itself for being able to handle unbounded uncertainty spaces. In fact, Ben-Haim (2001, 2006, 2010) indicates that indeed quite often this is the case in practice. It is therefore important to stress that in cases where the uncertainty space is unbounded and the problem is non-trivial, the size of the "safe neighborhood" is infinitesimally small (compared to the size of the uncertainty space). Therefore, it is perfectly legitimate to draw a very small white circle, as done above.