Local weather  
Brought to you by
 IF - IG 
International Interdisciplinary Center For
Information and Fact Checking about
Info-Gap Decision Theory

Local time
Home About News IGDT The Campaign Myths & Facts Reviews FAQs FUQs Resources Contact Us
The rise and rise of voodoo decision making

Reviews of publications on Info-Gap decision theory (IGDT)

Review 2-2022 (Posted: January 28, 2022; Last update: January 28, 2022)

Reference Yakov Ben-Haim. Chapter 5 Info-Gap Decision Theory (IG) in Vincent A. W. J. Marchau, Warren E. Walker, Pieter J. T. M. Bloemen. and Steven W. Popper (Editors), Decision Making under Deep Uncertainty. Springer.
Year of publication2019
Publication typeChapter in an open access book.
Downloads Publisher's website (Freely accessible PDF files, by chapter)
Abstract
  • Info-Gap(IG) Decision Theory is a method for prioritizing alternatives and making choices and decisions under deep uncertainty.
  • An "info-gap" is the disparity between what is known and what needs to be known for a responsible decision.
  • Info-gap analysis does not presume knowledge of a worst-case or of reliable probability distributions.
  • Info-gap models of uncertainty represent uncertainty in parameters and in the shapes of functional relationships.
  • IG Decision Theory offers two decision concepts: robustness and opportuneness.
  • The robustness of an alternative is the greatest horizon of uncertainty up to which that alternative satisfies critical outcome requirements.
  • The robustness strategy satisfices the outcome and maximizes the immunity to error or surprise. This differs from outcome optimization.
  • The robustness function demonstrates the trade-off between immunity to error and quality of outcome. It shows that knowledge-based predicted outcomes have no robustness to uncertainty in that knowledge.
  • The opportuneness of a decision alternative is the lowest horizon of uncertainty at which that decision enables better-than-anticipated outcomes.
  • The opportuneness strategy seeks windfalls at minimal uncertainty.
  • We discuss "innovation dilemmas" in which the decision maker must choose between two alternatives, where one is putatively better but more uncertain than the other.
  • Two examples of info-gap analysis are presented, one quantitative that uses mathematics and one qualitative that uses only verbal analysis.
ReviewerMoshe Sniedovich
Public Disclosure: 
To the best of my knowledge, the "local issue", the "maximin issue", as well as other issues, were first raised in writing in 2006, in the report What's wrong with info-gap? An Operations Research Perspective that was posted on my old website at Uni. The first peer-reviewed article on these "issues" was published in 2007 (see bibliography below). The Father of IGDT, Prof. Yakov Ben-Haim, is familiar with my criticism of his theory. Indeed, in 2007 he attended two of my lectures where I discussed in detail the major flaws in IGDT.
IF-IG perspective This is a typical IGDT publication in that it completely misjudges the role and place of IGDT in the state of the art in decision making under deep uncertainty. It also repeats unsubstantiated claims about IGDT, its capabilities and limitations, and its intimate relation to Wald's famous Maximin paradigm.

Reviewer's Comment

The reader is reminded that this is a review, not a tutorial. However, in view of the content of the chapter under review, it is necessary to discuss a lot of material that is not discussed openly in the IGDT literature, and to explain in detail certain technical issues. In particular, it is important to explain in detail (1) why IGDT is fundamentally flawed (2) why it is unsuitable for the treatment of deep uncertainties of the type it postulates, and (3) the fact that IGDT's robustness related models are simple maximin models. The end result is that, by necessity, parts of this review turned into sort of mini-tutorials. 
The reader is advised that most of the observations, facts, results and so on, discussed in this review, are not new. They have been published a long time ago. It is nevertheless necessary to go through them again because proponents of IGDT continue to ignore them even under the watching eyes and scrutiny of the revered peer-review process that is supposed to prevent this from happening.  
This review is intended primarily for readers who are really interested in understanding and appreciating the flaws in IGDT and the way it is presented in the literature, including peer-reviewed publications. It is particularly intended for referees and editors of peer-reviewed publications, who still believe that IGDT is a suitable theory for the treatment of severe uncertainty.  
Readers who are only interested in the bottom line, can read the preface and summary sections. 
I am fully aware of the fact that some readers may feel very strongly that this review is too harsh. To this I say that, in my humble opinion, the harshness of my criticism is fully justified and well deserved as it is a reflection of the current state of the art in IGDT. I'll be happy to change my view if proven wrong.  
The review often refers to the main three texts on IGDT, namely
  • Yakov Ben-Haim (2001). Information-gap Decision Theory: Decisions Under Severe Uncertainty. Academic Press.
  • Yakov Ben-Haim (2006). Info-gap Decision Theory: Decisions Under Severe Uncertainty, 2nd edition. Elsevier Science Publishing Co Inc.
  • Yakov Ben-Haim (2010). Info-Gap Economics An Operational Introduction. Palgrave Macmillan, UK.

Preface

It is not necessary to consider in detail all the erroneous and/or unsubstantiated claims made in this chapter (henceforth CHAPTER) about the role and place of IGDT in decision making under deep uncertainty. These details are discussed all over this site, in many reports and peer-reviewed articles, and in the old reviews of IGDT publications.

However!!!!!

The mere fact that the CHAPTER is included in an edited book that is dedicated to Decision Making Under Deep Uncertainty basically means that some, perhaps many, DMDU analysts and scholars still believe that IGDT is suitable for the treatment of deep uncertainty. This strongly influenced my decision (at the end of 2021) to revive the campaign to contain the spread of IGDT in Australia. As part of this campaign, in this review I discuss in detail, again, some of the issues that require attention regarding the role and place of IGDT in the state of the art in decision making under deep uncertainty.

By way of introduction, it suffices to mention these points about the CHAPTER:

  1. The CHAPTER does not mention the fact that IGDT's robustness is a reinvention of the well known and well established concept that is known universally as Radius of Stability.

  2. It continues to dispute the formally proven fact that IGDT's two core robustness related models are maximin models, hence the theory itself is essentially a Wald-type Maximin theory.

  3. It continues to spread serious misconceptions about what Wald-type maximin models are and what they can and cannot do.

  4. It continues to insist that IGDT is suitable for the treatment of severe uncertainties of the type postulated in Ben-Haim (2001, 2006, 2010), despite the fact that it is clearly not.

  5. It continues to ignore well-documented valid criticisms of IGDT.

For these reasons, it is surprising that the CHAPTER appears in an edited book whose stated goal is to provide the latest information about the state of the art in decision making under deep uncertainty. This issue is discussed in Review 1-2022.

As we shall see, the concept "radius of stability", also called "stability radius", plays an important role in this review. So, for the benefit of readers who are not familiar with this intuitive concept, here are some useful quotes:

The formulae of the last chapter will hold only up to a certain "radius of stability," beyond which the stars are swept away by external forces.
von Hoerner (1957, p. 460)

It is convenient to use the term "radius of stability of a formula" for the radius of the largest circle with center at the origin in the s-plane inside which the formula remains stable.
Milner and Reynolds (1962, p. 67)

The radius $r$ of the sphere is termed the radius of stability (see [33]). Knowledge of this radius is important, because it tells us how far one can uniformly strain the (engineering, economic) system before it begins to break down.
Zlobec (1987, p. 326)

An important concept in the study of regions of stability is the "radius of stability" (e.g., [65, 89]). This is the radius $r$ of the largest open sphere $S(\theta^{*}, r)$, centered at $\theta^{*}$, with the property that the model is stable, at every point $\theta$ in $S(\theta^{*}, r)$. Knowledge of this radius is important, because it tells us how far one can uniformly strain the system before it begins to "break down". (In an electrical power system, the latter may manifest in a sudden loss of power, or a short circuit, due to a too high consumer demand for energy. Our approach to optimality, via regions of stability, may also help understand the puzzling phenomenon of voltage collapse in electrical networks described, e.g., in [11].)
Zlobec (1988, p. 129)

Robustness, or insensitivity to perturbations, is an essential property of a control-system design. In frequency-response analysis the concept of stability margin has long been in use as a measure of the size of plant disturbances or model uncertainties that can be tolerated before a system loses stability. Recently a state-space approach has been established for measuring the "distance to instability" or "stability radius” of a linear multivariable system, and numerical methods for computing this measure have been derived [2,7,8,11].
Byers and Nichols (1993, pp. 113-114)

Robustness analysis has played a prominent role in the theory of linear systems. In particular the state-state approach via stability radii has received considerable attention, see [HP2], [HP3], and references therein. In this approach a perturbation structure is defined for a realization of the system, and the robustness of the system is identified with the norm of the smallest destabilizing perturbation. In recent years there has been a great deal of work done on extending these results to more general perturbation classes, see, for example, the survey paper [PD], and for recent results on stability radii with respect to real perturbations, see [QBR*].
Paice and Wirth (1998, p. 289)

The stability radius is a worst case measure of robustness. It measures the size of the smallest perturbation for which the perturbed system is either not well-posed or does not have spectrum in $\mathbb{C}_{g}$.
Hinrichsen and Prichard (2005, p. 585)

The radius of the largest ball centered at $\theta^{*}$ , with the property that the model is stable at its every interior point $\theta$, is the radius of stability at $\theta^{*}$, e. g., [69]. It is a measure of how much the system can be uniformly strained from $\theta^{*}$ before it starts breaking down.
Zlobec (2009, p. 2619)

Stability radius is defined as the smallest change to a system parameter that results in shifting eigenvalues so that the corresponding system is unstable.
Bingham and Ting (2013, p. 843)

Using stability radius to assess a system's behavior is limited to those systems that can be mathematically modeled and their equilibria determined. This restricts the analysis to local behavior determined by the fixed points of the dynamical system. Therefore, stability radius is only descriptive of the local stability and does not explain the global stability of a system.
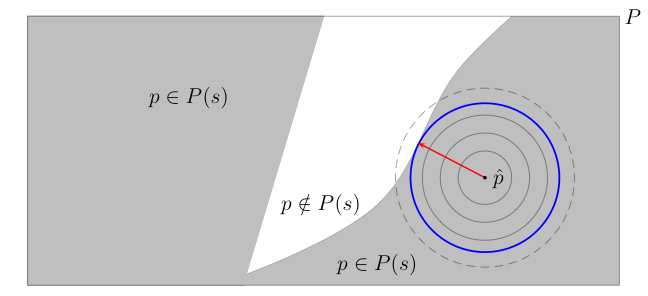
Bingham and Ting (2013, p. 846)

And here is the picture:

Here $P$ denotes the set of values parameter $p$ can take, $P(s)$ denotes the set comprising of parameter values where the system is stable (shown in gray), and the white region represent the set of parameter values where the system is unstable. The radius of stability of the system at $\widetilde{p}$ is equal to the shortest distance from $\widetilde{p}$ to instability. It is the radius of the largest neighborhood around $\widetilde{p}$ all whose points are stable.

Clearly, this measure of robustness is inherently local in nature, as it explores the immediate neighborhood of the nominal value of the parameter, and the exploration is extended only as long as all the points in the extended neighborhood are stable. By design then, this measure does not attempt to explore the entire set of possible values of the parameter. Rather, it focuses on the immediate neighborhood of the nominal value of the parameter. The expansion of the neighborhood terminates as soon as an unstable value of the parameter is encountered. So technically, methods based on this measure of robustness, such as IGDT, are in fact based on a local worst-case analysis.

Note that under deep uncertainty the nominal value of the parameter can be substantially wrong, even just a wild guess. Furthermore, in this uncertain environment there is no guarantee that "true" value of the parameter is more likely to be in the neighborhood of the nominal value than in neighborhood of any other value of the parameter. That is, such a local analysis cannot be justified on the basis of "likelihood", or "plausibility", or "chance", or "belief" regarding the location of the true value of the parameter, simply because under deep uncertainty the quantification of the uncertainty is probability, likelihood, plausibility, chance, and belief FREE!.

Awareness and appreciation of the fact that "IGDT robustness" is a reinvention of the concept "radius of stability" are necessary for a proper assessment of the role and place of IGDT in the state of the art in decision making under deep uncertainty. It is important to stress that in all the above quoted cases, the radius of stability is used as a measure of local stability/robust, that is stability/robustness against small perturbation in a nominal value of a parameter.

One of the conclusions of this review is that it is time for the "DMDU community" to realize and acknowledge the fact that the concept "IGDT robustness" is a reinvention of the well established concept "radius of stability".

This review focuses on the Maximin connection, as this will provide a good framework for figuring out in what sense the CHAPTER is so wrong about the role and place of IGDT in the state of the art in decision making under severe uncertainty. With this in mind, let us introduce the Elephant in the Room, and ask the following important question that proponents of IGDT pretend does not exit:

Are IGDT's two core robustness related models Wald-type Maximin models?

In fact, in view of what the peer-reviewed literature tells us about IGDT, it is more appropriate to phrase the question this way:

Aren't IGDT's two core robustness related models Wald-type Maximin models?!

In any case, the interesting things is that answers to these and similar questions have been available for everyone to read, including onboard this site, at least since 2006. Yet, it is necessary to address them again in 2022. The point is that the definitive answer to the above questions is crystal clear:

Definitely Yes!
IGDT's two core robustness related models are simple Wald-type Maximin models. The two opportuneness related models are Minimin models, hence ordinary minimization models. They are based on the assumption that, from the decision maker point of view, Nature (namely uncertainty) is a benevolent agent.

The main goal of this review is to draw the attention of IGDT users and potential new users to well documented details regarding the role and place of IGDT in the state of the art in decision making under uncertainty. The key points are:

By necessity this review is pretty long, so for the reader's convenience, here is a table of contents. Readers who are not interested in the technical aspects of the discussion can skip the formal sections.

IGDT's four core models

IGDT is based on and uncertainty model and four core models involving decision making. Our interest lies primarily in the two robustness related decision models. The two opportuneness related models are examined only briefly because, from a decision-making under deep uncertainty point of view, they are extremely simplistic, as they are implementations of the overly optimistic approach to deep uncertainty guided by the rule: If uncertain, assume the best! We do briefly explain, though, why these two models are of little interest to us in this review.

These four models are built around a very austere uncertainty model that for the purposes of this discussion can be described as follows:

$$ \begin{align} u & = \text{uncertainty parameter,}\tag{U-1}\\ \mathscr{\overline{U}} & = \text{uncertainty space,}\tag{U-2}\\ \widetilde{u} & = \text{given nominal value of $u$,}\tag{U-3}\\ \mathscr{U}(\alpha,\tilde{u}) & = \text{neighborhood of size ("radius") $\alpha$ around $\widetilde{u}$.} \tag{U-3} \end{align} $$
Assumption. As usual, the neighborhoods are "nested", namely $\mathscr{U}(0,\widetilde{u}) = \{\widetilde{u}\}$ and $\alpha\,' \le \alpha\,''$ implies that $\mathscr{U}(\alpha\,',\widetilde{u}) \subseteq \mathscr{U}(\alpha\,'',\widetilde{u})$. With no loss of generality we can assume that $\mathscr{\overline{U}} = \mathscr{U}(\infty,\widetilde{u})$.

Note that although this model is abstract, it is highly structured. The severity of the uncertainty is due to the fact that the neighborhoods can be very large; the nominal value $\widetilde{u}$ can be substantially wrong; and, most importantly, the model lacks any measure of 'likelihood', or 'plausibility' , or 'chance', or 'belief' as to where the true (unknown) value of $u$ is located in $\mathscr{\overline{U}}$. By all accounts, such a severe uncertainty qualifies as being deep.

Imposed on this uncertainty model are four core models involving a decision variable. This is what makes IGDT a decision theory. Two models deal with robustness and two with opportuneness. Here they are the way they are often presented in the IGDT literature:

$$ \hspace{-200px}\begin{align} \alpha^{*}(d):& = \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq \min_{u\in \mathscr{U}(\alpha,\widetilde{u})}\ r(d,u)\big\} \ , \ d\in D \ \ \ \text{(robustness model) }\tag{IGRM}\\ \beta^{*}(d):& = \min_{\beta \geq 0} \ \big\{\beta: r_{w}\leq \max_{u\in \mathscr{U}(\beta,\widetilde{u})}\ r(d,u)\big\} \ , \ d\in D\ \ \text{ (opportuneness model)} \tag{IGOM}\\ \alpha^{**}:& = \max_{d\in D} \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq \min_{u\in \mathscr{U}(\alpha,\widetilde{u})}\ r(d,u)\big\} \ \ \ \ \ \ \ \, \text{ (robust-satisficing decision model) } \tag{IGRSDM}\\ \beta^{**}:& = \min_{d\in D} \min_{\beta \geq 0} \ \big\{\beta: r_{w}\leq \max_{u\in \mathscr{U}(\beta,\widetilde{u})}\ r(d,u)\big\} \ \ \ \ \ \ \ \ \ \text{ (opportune-satisficing decision model)} \tag{IGOSDM}\\ \text{In these models:     } & \ \ \notag\\ d & = \text{ decision variable,}\tag{1}\\ u & = \text{ uncertainty parameter whose true value is unknown,}\tag{2} \\ \widetilde{u} & = \text{ a given nominal value of $u$ regarded as an estimate of the true value of $u$,}\tag{3}\\ D &= \text{ decision space,}\tag{4}\\ \mathscr{U} (\rho, \widetilde{u}) & = \text{ neighborhood of uncertainty of size (radius) $\rho$ around $\widetilde{u}$, }\tag{5}\\ r(d,u) & = \text{ performance level of decision $d$ if the true value of the uncertainty parameter is equal to $u$, } \tag{6}\\ r_{c}, r_{w} & = \text{ given critical performance levels.} \tag{7}\\ \alpha^{*}(d) & = \text{robustness of decision $d$}\tag{8}\\ \beta^{*}(d) & = \text{opportuneness of decision $d$}\tag{9} \end{align} $$
Assumption:
With no loss of generality it is convenient to assume that in the robustness related models $r_{c} \leq r(d,\widetilde{u}), \forall d\in D$ and in the opportuneness related models $r_{w} > r(d,\widetilde{u}), \forall d\in D$.

A deep uncertainty perspective

Based on the structure of its core models, it is not clear at all why IGDT is viewed as a decision theory for decision making under deep uncertainty. It models address questions that have absolutely nothing to do with deep uncertainty, so the answers they provide for these questions do not address the difficulties posed by deep uncertainty. More specifically, IGDT addresses the following questions:

Suppose that we find that decision $d'$ is more robust than decision $d''$ at $\widetilde{u}$. Does this mean that $d'$ is more robust than $d''$ at other points in the uncertainty space? If not, in what sense do the above models address the difficulty posed by deep uncertainty?

It is very easy to construct examples where a decision is very robust locally, but very fragile elsewhere on the uncertainty space.

In summary:

The last point was discussed in writing as early as 2006, and in peer reviewed journals as early as 2007. In this review we are interested primarily in the two robustness related models, namely (IGRM) and (IGRSDM).

In view of the above, it is important to remind ourselves of one of the challenges posed by deep uncertainty that is relevant to the above discussion.

Under deep uncertainty there is no reason to assume that the true value of the uncertainty parameter is in the neighborhood of $\widetilde{u}$, or any other value of $u$. Therefore, to determine how well/badly a decision performs, it is necessary to examine the entire uncertainty space, or at least a sufficiently large sample of points from this space that adequately represent the variability of the parameter over this space.

The bottom line is that there is a big difference betweenlocal and global robustness, akin to the difference between local and global optimization, local vs general anesthesia, local vs global news, local vs global weather, and so on. A proper treatment of deep uncertainty requires a global analysis, or exploration, of the uncertainty space.

As indicated above, IGDT's core models are inherently local in nature. Therefore IGDT is not suitable for the treatment of deep uncertainty.

A gentle introduction to Wald's Maximin paradigm

The arguments used in the CHAPTER to support the mistaken assertion that IGDT robust decision model is not a maximin model are based on deep misconceptions about two basic modeling concepts, namely the relation between a prototype model and its instances. More specifically, the relation between prototype maximin models and the numerous instances derived from them. Understanding this relation is crucial to understanding why IGDT's robustness related models are simple Wald-type maximin models. For it turns out that these IGDT models are indeed simple instances of prototype Wald-type maximin models.

So let us clarify first what we mean by "maximin model" and "Wald-type maximin model" in the context of decision-making environments. The basic ingredients of these maximin models are as follows:

$$ \begin{align} x &= \text{decision (control) variable,}\tag{W-1} \\ s &= \text{state variable,}\tag{W-2}\\ X &= \text{decision space,}\tag{W-3} \\ \mathcal{S} & = \text{ state space,}\tag{W-4}\\ S(x) &= \text{ state space associated with decision $x$, (a subset of $\mathcal{S}$)}\tag{W-5}\\ f &= \text{ real-valued objective function on $X\times \mathcal{S}$.}\tag{W-6}\\ \text{constraints-on-($x,s$)} & = \textrm{ list of finitely many constraints on (decision,state) pairs.}\tag{W-7} \end{align} $$
Assumptions:
  • The decision maker (DM) plays first and tries to maximize the objective function $f$, subject to the constraints, by controlling the value of $x$.
  • In response a malevolent agent, call it MA, selects the worst value of $s$ (w.r.t the selected value of $x$).
  • This `game' is played once.

The two decision questions are:

The maximin approach to these decision problems is based then on the worst-case analysis 'rule' dictating that each decision by DM should be assessed on the basis of its worst performance. Hence, the best decision (for DM) is one whose worst performance is at least as good (large) as the worst performance of any other decision.

In his book A Theory of Justice Rawls described this rule as follows:

The maximin rule tells us to rank alternatives by their worst possible outcomes: we are to adopt the alternative the worst outcome of which is superior to the worst outcome of the others.
Rawls (1971, p. 152)

There are numerous other formal, and informal, descriptions of this rule. Observe that Rawls' phrasing of the rule does not make any reference to constraints. Since we assume that the greater $f(x,s)$ the better, it is clear what 'worst' means with regard to the objective function $f$: it means the smallest value of $f(x,s)$ over all values of $s$ in $S(x)$. But what about the constraints? How do we incorporate constraints in the framework of this rule?

The answer is this: since making the constraints stricter can only make the worst case even worse, or leave it as bad as it is (it cannot make it better), the worst case is the one where we require each decision to satisfy all the constraints imposed on it for all the associated values of the state variable. Thus, in the context of the maximin paradigm, the worst-case analysis imposes the following worst-case constraints on the decision variable $x$:

$$ \text{constraints-on-($x,s$)} \ , \ \color{red}\forall s\in S(x). \tag{worst-case constraints} $$

That is, in the maximin framework, decision $x$ is deemed feasible iff it satisfies all the constraints for all the states associated with it. Therefore, according to the maximin paradigm, the decision problem under consideration can be stated as follows:

$$ z^{*}:= \max_{x\in X}\min_{s\in S(x)} \ \big\{ f(x,s): \text{constraints-on-($x,s$)}, \color{red}\forall s\in S(x)\big\}\tag{P-Maximin} $$

Now to the question of what we mean by 'Wald-type maximin model'.

What exactly is a Wald-type maximin model? 
A Wald-type maximin model is a maximin decision model where the state variable represents uncertainty in the sense that its "true" value is unknown, except that it is an element of the state space $\mathcal{S}$. More specifically, for each $x\in X$ the state space $S(x)$ is the set of all possible value of $s$ given that the decision maker selects decision $x$. The uncertainty in the true value of $s$ is non-probabilistic, that is, it cannot be quantified by probability measures.

The point of this clarification is to stress that maximin models are used extensively in situations that have nothing to do with decision making under uncertainty. The idea of applying the maximin rule as a way of dealing with severe non-probabilistic uncertainty in the context of decision making situations was proposed by the mathematician Abraham Wald (1902-1950) in an article published in 1939, and since then it has been adopted in many fields, including decision theory, statistics, robust control, operations research, robust optimization, finance, economics, and so on. Needless to say, the maximin models used today are generalizations of Wald's early models. They are all based, though, on the dictum: "if uncertain, assume the worst!".

It is important to stress that (P-Maximin) is a very rich and powerful Prototype model. This is so due to the fact that the model's mathematical ingredients, namely the sets $X$, $\mathcal{S}$, $S(x), x\in X$, function $f$ and the list of constraints specified by $\text{constraints($x,s$)}$, are described only in very broad terms. This versatile prototype model therefore has a wide range of diverse instances. Let us examine two of these.

In simple situations where there are no constraints on $(x,s)$ pairs, the list of constraints specified by set $\text{constraints-on-($x,s$)}$ is empty and therefore (P-Maximin) simplifies to the following unconstrained version of (P-Maximin).

$$ z^{*}:= \max_{x\in X}\min_{s\in S(x)} \ f(x,s)\tag{U-P-Maximin} $$

Next, in many situations the objective function $f$ does not depend on the state variable $s$. Thus, formally in these situations $f$ is a real-valued function on $X$, hence we write $f(x)$ instead of $f(x,s)$. Since the operation $\displaystyle \min_{s\in S(x)}$ is superfluous under these conditions, (P-Maximin) simplifies to

$$ z^{*}:= \max_{x\in X} \ \big\{ f(x): \text{constraints-on-($x,s$)}, \color{red}\forall s\in S(x)\big\}\tag{MP-P-Maximin} $$

Models of this type are very popular in mathematical programming and robust optimization. The disappearance of the iconic $\displaystyle \min_{s\in S(x)}$ operation merely means that in such models the worst-case analysis is conducted only with respect to the constraints, as the objective function does not depend on $s$.

The following observation is intended for readers who still believe that IGDT's two core robustness related models are not Wald-type maximin models.

Any proper instance of a maximin model is a maximin model, and similarly any proper instance of a Wald-type maximin model is a Wald-type maximin model.  
A proper instance of a prototype model is an instance of the prototype model that satisfies the conditions imposed on the prototype model.

It is therefore important to be crystal clear about the conditions imposed on the three prototype maximin models formulated above, in particular on (P-Maximin). So let us start with (P-Maximin), recalling that in the framework of this model we have:

$$ \begin{array}{c || l } \text{Object} & \text{Requirements on (P-Maximin) and its instances}\\ \hline x & \text{decision variable,}\\ s & \text{uncertain state variable,}\\ X& \text{non-empty set,}\\ \mathcal{S}&\text{non-empty set,} \\ S(x)&\text{non-empty subset of $\mathcal{S}$,}\\ f&\text{real valued function on $X\times \mathcal{S}$},\\ \text{constraints-on-($x,s$)} & \text{list of finitely many constraints on $(x,s)$ pairs.}\\ &\text{It can be empty (no constraints on $(x,s)$ pairs).} \end{array} $$

Therefore, any instance of (P-Maximin) that satisfies these requirements is a proper instance. For example, both (U-P-Maximin) and (MP-P-Maximin) are proper instances of (P-Maximin). By inspection, (U-P-Maximin) is the instance of (P-Maximin) characterized by the property that the list of constraints, namely $\text{constraints($x,s$)}$, is empty, and (MP-P-Maximin) is the instance of (P-Maximin) characterized by the property that the objective function does not depend on the state variable.

The reader should be advised that sometime a bit of manipulation and reformulation are required to show that the required properties are satisfied. To illustrate, consider the following two cases:

$$ \begin{align} z:&= \max_{x\in X} \ \big\{f(x): c \le \min_{s\in S(x)} g(x,s)\big\} \tag{Case 1}\\ z:&= \max_{x\in X} \ \big\{f(x): c \le \max_{s\in S(x)} g(x,s)\big\} \tag{Case 2} \end{align} $$

where $c$ is a real number and $g$ is a real-valued function on $X\times \mathcal{S}$. Are these models maximin models? If so, what is/are the respective prototype maximin model(s) from which these instances can be derived?

By inspection, since in these cases the objective function does not depend on the state variable, it makes sense to relate these models to (MP-P-Maximin). So to decide on this matter we have to examine the constraints. Utilizing the definition of the $\min$ and $\max$ operations, we reformulate the constraints and restate these models as follows:

$$ \begin{align} z:&= \max_{x\in X} \ \big\{f(x): c \le g(x,s)\ , \ \color{red}\forall s\in S(x)\big\} \tag{Case 1}\\ z:&= \max_{x\in X} \ \big\{f(x): c \le g(x,s) \text{ for at least one $s\in S(x)$} \big\} \tag{Case 2} \end{align} $$

By inspection, Case 1 is clearly a proper instance of (MP-P-Maximin). How about Case 2?

Observe that in this case the constraint is not a worst-case constraint, but a best-case constraint: for decision $x$ to be deemed feasible it is sufficient that it satisfies the constraint for a single value of $s$. In fact, it is possible to eliminate the clause "for at least one $s\in S(x)$" and reformulate the problem as follows: $$ \begin{align} z:&= \max_{x\in X}\max_{s\in S(x)} \ \big\{f(x): c \le g(x,s)\big\} \tag{Case 2}\\ & = \max_{x\in X, s\in S(x)} \ \big\{f(x): c \le g(x,s) \big\} \end{align} $$

Note that this formulation forces the decision maker and Nature to select a pair $(x,s)$ such that $x$ satisfies the constraint for the selected value of $s$.

In short, this Case 2 is a Maximax model: not only that Uncertainty is not an adversary here, it in fact is cooperating with the decision maker is her attempt to maximize the objective function. Indeed, we can regard $s$ as an auxiliary decision variable that is control by the decision maker, and view $y=(x,s)$ as the active decision variable. The problem can therefore be viewed as a "conventional" maximization problem where the decision variable consists of two components. Differently put, the state variable is now 'controlled' by the decision maker, rather than by Nature (equivalently: Nature is cooperating fully with the decision maker).

We are ready to reexamine IGDT's four core models. But before we do that, an important maximin modeling warning/ advice/ tip:

A useful maximin modeling tip: 
The three maximin models discussed above, namely (P-Maximin), (U-P-Maximin), and (MP-P-Maximin) are 'equivalent' in the sense that their respective formats are interchangeable: any problem that can be modeled by one of these models, can also be modeled by the other two models. In practice, the choice between these models is a matter of style and convenience. To illustrate, consider this maximin model:

$$ z^{*}:= \max_{x\in X} \min_{s\in S(x)} \big\{f(x,s): g(s,x) \ge c, \forall s\in S(x)\big\} $$

By inspection, this is a simple instance of (P-Maximin). It is characterized by the fact that both the objective function and the constraint function $g$ depend on the state variable $s$.

Now, consider this close relative of the above model:

$$ z^{**}:= \max_{x\in X, t\in \mathbb{R}} \big\{t: t \le f(x,s), g(s,x) \ge c, \forall s\in S(x)\big\} $$

where $\mathbb{R}$ denotes the real line. Note that in the framework of this model the decision variable is the pair $(x,t)$.

Since the objective function does not depend on the state variable, this model can be classified as a (MP-P-Maximin) type model.

But a closer examination of these two models reveals that they are 'equivalent' in the sense that $z^{*}=z^{**}$ and $x^{*}$ is an optimal value of $x$ in one model iff it is also an optimal value of $x$ in the other.

This useful trick is used extensively in situations where there is a need to transform a (P-Maximin)-type model into an 'equivalent' (MP-P-Maximin) model.

An informal look at IGDT's core models

Recall that IGDT's two core robustness related models are as follows:

$$ \hspace{0px}\begin{align} \alpha^{*}(d):& = \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq \min_{u\in \mathscr{U}(\alpha,\widetilde{u})}\ r(d,u)\big\} \ , \ d\in D \ \ \ \text{(robustness model) }\tag{IGRM}\\ \alpha^{**}:& = \max_{d\in D} \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq \min_{u\in \mathscr{U}(\alpha,\widetilde{u})}\ r(d,u)\big\} \ \ \ \ \ \ \ \, \text{ (robust-satisficing decision model) } \tag{IGRSDM} \end{align} $$

As was done above in Case 1 and Case 2, the models can be reformulated as follows:

$$ \hspace{0px}\begin{align} \alpha^{*}(d):& = \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq r(d,u)\ , \ \color{red}\forall u\in \mathscr{U}(\alpha,\widetilde{u})\big\} \ , \ d\in D \ \ \ \text{(robustness model) }\tag{IGRM}\\ \alpha^{**}:& = \max_{d\in D} \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq r(d,u)\} \ , \ \color{red}\forall u\in \mathscr{U}(\alpha,\widetilde{u})\big\} \ \ \ \ \ \ \text{ (robust-satisficing decision model) } \tag{IGRSDM}\\ & = \max_{d\in D, \alpha \geq 0} \ \big\{\alpha: r_{c}\leq r(d,u)\} \ , \ \color{red}\forall u\in \mathscr{U}(\alpha,\widetilde{u})\big\} \end{align} $$

Hence, by inspection, we conclude that these two models are proper instances of (MP-P-Maximin), observing that in the context of the robustness model $\alpha$ plays the role of a decision variable ($d$ in treated as a given parameter); and in the context of the robust-satisficing decision model $\alpha$ plays the role of an auxiliary decision variable, so the active decision variable is $y=(d,\alpha)$.

In the case of the two opportuneness based models, after we modify them a long the same lines, we can reformulate them as follows:

$$ \hspace{0px}\begin{align} \beta^{*}(d):& = \min_{\beta \geq 0, u\in \mathscr{U}(\beta,\widetilde{u})} \ \big\{\beta: r_{w}\leq r(d,u)\big\} \ , \ d \in D\ \ \text{ (opportuneness model)} \tag{IGOM}\\ \beta^{**}:& = \min_{d\in D,\beta \ge 0, u\in \mathscr{U}(\beta,\widetilde{u})} \ \big\{\beta: r_{w}\leq r(d,u)\big\} \ \ \ \ \ \ \ \ \,\text{ (opportune-satisficing decision model)} \tag{IGOSDM} \end{align} $$

The conclusion therefore is that, as in Case 2 above, these two models are definitely not Maximin models: they are Minimin models in which uncertainty is a benevolent agent that cooperates fully with the decision maker. This is due to the fact that the constraints are not worst-case type, but rather best-case type.

In summary:

A short informal examination of IGDT's four core models seems to suggest the following:
  • The two robustness related models are simple Wald-type maximin models, specifically they can be easily derived by instantiating (MP-P-Maximin).

  • The two opportuneness related models are simple Minimin models, as they are based on a best-case analysis of the constraints.

We need a break.

An informal time out!

All IGDT's core models are optimization problems: the decision maker attempts to optimize a measure of performance. The robustness related models are maximization problems and the opportuneness related models minimization problems. A quick inspection of these models reveals that in all these models the objective functions are independent of the uncertainty parameter $u$.

The implication of this simple observation is that in these models the real action takes place in the constraints. And a quick examination of the robustness constrains immediately reveals that these constraints are worst-case type of constraints: they do the best they can to prevent the decision maker from increasing the value of $\alpha$ (the size (radius) of the uncertainty neighborhood around the best guess $\widetilde{u}$).

And so, in the robustness case, the picture is this: the decision maker is trying to increase the value of $\alpha$, while Uncertainty tries to prevent her from doing so by imposing a worst-case analysis of the constraints. This fits Wald (1945) narrative that Wald-type maximin models can be viewed as games where the decision maker plays against Nature (= uncertainty).

The situation is radically different in the context of the opportuneness model: here the decision maker tries to make $\beta$ as small as possible and Uncertainty is fully cooperating with her. That is, Uncertainty approves the value of $\beta$ as soon as one single value of $u$ satisfies the performance constraint. This is a classic Minimin situation.

In short, as Richard Bellman (1920-1984), the Father of Dynamic Programming, used to say, "The rest is mathematics and experience!"

So let us reexamine the mathematics of IGDT.

A formal look at IGDT's core models

The objective of this section is two fold. First, to release, once and for all, the poor Elephant from the IGDT literature by proving formally and rigorously, yet again, that IGDT's two core robustness related model are simple Wald-type maximin models. Second, to explain, yet again, why IGDT is unsuitable for the treatment of deep uncertainty of the type it postulates and why it can be regarded as a voodoo decision theory par excellence.

Before we begin with the formal proof, it is necessary to stress the following point. There is a huge difference between the formal mathematical models, that together lay the foundation for IGDT, and the rhetoric about the theory, what it does, its role and place in the state of the art, its relation to other theories, and so on. The important issue of the rhetoric is discussed briefly in the next section. In this section we deal exclusively with IGDT's core mathematical models as they are presented in numerous publications, including the three books by Ben-Haim (2001, 2006, 2010).

So here we go!

Theorem. 
Both IGDT's robustness model and IGDT's robust-satisficing decision model are simple Wald-type maximin models.

We provide two proofs.

Proof No. 1

Consider the two instances of (MP-P-Maximin) specified as follows:

(MP-P-Maximin) $$ \displaystyle z^{*}:= \max_{x\in X}\ \big\{f(x): \text{constraint-on-($x,s$)} \ , \ \forall s\in S(x)\big\} $$
$$ \begin{array} {c | | c c } \text{(MP-P-Maximin) Object} & \text{    Instance 1    } & \text{    Instance 2    } \\ \hline x & \alpha & (d,\alpha) \\ s & u & u \\ X & [0,\infty) & D\times [0,\infty)\\ S(x) & \mathscr{U}(\alpha,\widetilde{u}) & \mathscr{U}(\alpha,\widetilde{u})\\ \mathcal{S} & \mathscr{U}(\infty,\widetilde{u}) & \mathscr{U}(\infty,\widetilde{u})\\ f(x) & \alpha & \alpha\\ \text{constrains-on-($x,s$)} & \ \ \ \ \ r_{c} \le r(d,u)\ \ \ \ \ &\ \ \ \ \ r_{c} \le r(d,u)\ \ \ \ \ \end{array} $$

Note: in the two instances, $\widetilde{u}$ is given. In Instance 1, $d$ is given.

The instantiation of (MP-P-Maximin) specified by Instance 1 yields IGDT's robustness model and the instantiation of (MP-P-Maximin) specified by Instance 2 yields IGDT's robust-satisficing decision model. $\blacksquare$

Proof No. 2

This proof is a step by step implementation of Proof No. 1, where the instantiation is done gradually. It is provided for the benefit of readers who are not familiar with instantiations of this type. We conduct the specified instantiation gradually, step by step, where in each step the instantiation is made on the maximin model resulting from the previous step. The steps are as follows:

  • Step 1: Instantiate $x$, $s$ and $X$.

  • Step 2: instantiate S(x) and f(x).

  • Step 3: Instantiate $\text{ constraints-on-($x,s$)}$.

Part A: Instance 1:

$$ x=\alpha; \ \ s=u; \ \ X = [0,\infty);\ \ S(x) = \mathscr{U}(\alpha,\widetilde{u}); \ \ f(x) = \alpha;\ \ \text{constraints-on-(x,s)} = \{ r_{c} \le r(d,u)\} $$

Step 1 yields: $\ \ \ \ \displaystyle z^{*}:= \max_{\alpha\ge 0}\ \big\{f(\alpha): \text{constraint-on-($\alpha,u$)} \ , \ \forall u\in S(\alpha)\big\} $

Step 2 yields: $\ \ \ \ \displaystyle z^{*}:= \max_{\alpha\ge 0}\ \big\{\alpha: \text{constraint-on-($\alpha,u$)} \ , \ \forall u\in \mathscr{U}(\alpha,\widetilde{u})\big\} $

Step 3 yields: $\ \ \ \ \displaystyle z^{*}:= \max_{\alpha\ge 0}\ \big\{\alpha: r_{c}\le r(d,u) \ , \ \forall u\in \mathscr{U}(\alpha,\widetilde{u})\big\} $

This is no other than IGD's robustness model. $\blacksquare$

Part B: Instance 2

$$ x=(d,\alpha); \ \ s=u; \ \ X = D\times [0,\infty);\ \ S(x) = \mathscr{U}(\alpha,\widetilde{u}); \ \ f(x) = \alpha;\ \ \text{constraints-on-($x,s$)} = \{ r_{c} \le r(d,u)\} $$

Step 1 yields: $ \ \ \ \ \displaystyle z^{*}:= \max_{d\in D, \alpha\ge 0}\ \big\{f(d,\alpha): \text{constraint-on-($(d,\alpha),u$)} \ , \ \forall u\in S(d,\alpha)\big\} $

Step 2 yields: $\ \ \ \ \displaystyle z^{*}:= \max_{d\in D, \alpha\ge 0}\ \big\{\alpha: \text{constraint-on-($(d,\alpha),u$)}\big\} \ , \ \forall u\in \mathscr{U}(\alpha,\widetilde{u})\big\} $

Step 3 yields: $\ \ \ \ \displaystyle z^{*}:= \max_{d\in D, \alpha\ge 0}\ \big\{\alpha: r_{c} \le r(d,u)\ , \ \forall u\in \mathscr{U}(\alpha,\widetilde{u})\big\} $

This is no other than IGDT's robust-satisficing decision model. $\blacksquare$

IGDT's robustness model being IGDT's flagship calls for a closer examination of this simple maximin model:

$$ \begin{align} \alpha^{*}(d):& = \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq \min_{u\in \mathscr{U}(\alpha,\widetilde{u})}\ r(d,u)\big\} \ , \ d\in D \ \ \ \text{(robustness model) }\tag{IGRM}\\ & = \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq r(d,u) \ , \ \color{red} \forall u \in \mathscr{U}(\alpha,\widetilde{u}) \big\} \end{align} $$

Since in this setup $d$ is given, it is instructive to hide it and consider instead the following simpler looking maximin model:

$$ \alpha^{\circ}: = \max_{\alpha \geq 0} \ \big\{\alpha: r_{c}\leq g(u) \ , \ \color{red} \forall u \in \mathscr{U}(\alpha,\widetilde{u}) \big\}\tag{Mystery Model} $$

where $g(u)=r(d,u)$.

It is time now to examine closely an extremely important feature of IGDT that casts a dark shadow over the official IGDT rhetoric concerning the role and place of the theory in the state of the art in decision-making under deep uncertainty.

Reminder: 
In the framework of (Mystery Model)
$$ \begin{align} \widetilde{u} &= \text{ nominal value of the uncertainty parameter $u$}\tag{About $\widetilde{u}$} \\ \mathscr{U}(\alpha,\widetilde{u}) & = \textbf{neighborhood} \text{ of size (radius) $\alpha$ around $\widetilde{u}$ } \tag{About $\mathscr{U}(\alpha,\widetilde{u})$} \end{align} $$

Two important observations immediately come to mind regarding (Mystery Model) hence IGDT:

  1. (Mystery Model) is a simple Radius of Stability model.  
  2. As such the model is inherently local in nature.

The immediate implications of these two observations deserve careful attention. The first implies that IGDT's flagship idea, namely IGDT Robustness, is no more than a reinvention of a well known and well established measure of local stability/robustness that is universally known as Radius of Stability or Stability Radius whose origin dates back to the 1960s. This fact about IGDT was observed and documented in 2010. For some strange reason proponents of IGDT continue to ignore this important feature of IGDT.

The immediate implication of the second observation is that IGDT is unsuitable for the treatment of severe uncertainties of the type it stipulates. The picture is this:

The black rectangle represents the uncertainty space and the small yellow square represent the largest neighborhood around the point estimate over which a decision satisfies the performance constraint. Very close to the boundary of the square, in the black area, there is a point where the decision violates the constraint. Therefore, it is impossible to increase the size of the small square (along the two axes) without violating the constrains. Hence, the size of the small square is the radius of stability (IGDT robustness) of the decision under consideration. We have no idea how well/badly the decision performs over the large black area. Indeed, IGDT makes no attempt to explore the black area to determine how well/badly the decision performs in areas at a distance from the small yellow square. Clearly therefore, IGDT's measure of robustness is a measure of local robustness. For obvious reasons, such a measure of robustness is not suitable for the treatment of deep uncertainty.

One of the challenges posed by deep uncertainty is the need to explore a vast and diverse uncertainty space to determine how well/badly decisions perform over this space. Note that IGDT prides itself for being able to cope with unbounded uncertainty spaces. In such cases, the small yellow square will be infinitesimally small compared to the black area. I refer to the black area as the No-man's Land of IGDT's robustness analysis.

In short, what emerges then is this:

IGDT's secret weapon for dealing with deep uncertainty: 
Ignore the severity of the uncertainty! Conduct a local analysis in the neighborhood of a poor estimate that may be substantially wrong, perhaps even just a wild guess. This magic recipe works particularly well in cases where the uncertainty is unbounded! 
The obvious flaws in the recipe should not bother you, and definitely should not prevent you from claiming that the method is reliable! To wit (color is used for emphasis):
The management of surprises is central to the “economic problem”, and info-gap theory is a response to this challenge. This book is about how to formulate and evaluate economic decisions under severe uncertainty. The book demonstrates, through numerous examples, the info-gap methodology for reliably managing uncertainty in economic policy analysis and decision making.
Ben-Haim (2010, p. x)

And I ask:

How can a methodology that ignores the severity of the uncertainty it is supposed to deal with, possibly provide a reliable foundation for economic policy and decision making under such an uncertainty?

Despite the fact that the inherent local orientation of IGDT is well documented (at least since 2006), many publications continue to present IGDT as a theory for decision making under severe or deep uncertainty. The CHAPTER is a typical example.

Readers who are not familiar with the distinction between global and local robustness are encouraged to read the discussions on this subject on this site here and here.

We need a time out.

A formal time out!

Since mathematically speaking the structure of maximin models is quite simple and straightforward, and since it is clear as a daylight that IGDT's two core robustness related models are simple instances of a simple prototype maximin model, the following question arises:

On what basis do proponents of IGDT claim that these models are not maximin models?

When you examine the IGDT literature carefully, you discover that claims insisting that IGDT's robustness related models are not maximin models are based on a serious misconception about the modeling of decision making problems in general, and mathematical modeling in particular, as well as some elementary technical issues regarding the existence of a worst-case. This review focuses on the modeling issue.

For some unknown reasons, from the very beginning (circa 2001), the IGDT literature refused to acknowledge the fact that optimization theory can deal with decision making problems where constraints are imposed on the problem, and that optimization theory provides tools for dealing with uncertainty and robustness against uncertainty.

In fact, some passages in the IGDT literature read as if IGDT has complete monopoly on constraints satisfaction and robustness, and the very active field of Robust Optimization does not exist. In particular, the IGTD literature apparently is of the opinion that it will never cross the mind of users of maximin or minimax models to include robustness against violation of constraints in their models. In fact, the IGDT literature seems to assume that users of maximin or minimax models actually cannot incorporate such constraints in their models because these models are incapable of dealing with such constraints.

To illustrate this point, consider the comparison conducted in the article Profiling for crime reduction under severely uncertain elasticities (Davidovitch and Ben-Haim, 2008) between the following IGDT robust-satisficing decision model and a related minimax decision model:

$$ \begin{array} {c|c} \text{minimax model} & \text{Robust-satisficing decision model}\\ \hline \displaystyle \min_{q\in \mathit{Q}}\max_{u\in \mathscr{U}(\alpha_{m}, \widetilde{u})} L(q,u) & \displaystyle \max_{q\in \mathit{Q}} \max_{\alpha\ge 0} \big\{\alpha: L_{c} \ge L(q,u) \ , \ \forall u\in \mathscr{U}(\alpha, \widetilde{u}) \big\} \end{array}\tag{Two Models} $$

These two models, it is argued in the article, represent two different approaches to the problem discussed in the article. The minimax model describes how the minimax/maximin paradigm views the problem, and the robust-satisficing decision model describes how IGDT's robust-satisficing approach views the problem. The article conclude that although there are some similarities, the two models are different.

The article's entire discussion on these two models is bizarre. First, it is clear that the two models do not represent the same problem, hence it is unclear what is the rationale for the comparison. Second, it is not clear at all on what basis the article determined that the minimax model represents the maximin/minimax paradigm's view of the problem under consideration. Since the constraint $L_{c} \ge L(q,u)$ is important, it is necessary to include it in the model, and it is not clear at all why the anonymous minimax modeler who formulated the minimax model shown above, decided not to do it. In short, the article does not tell us anything as to why the constraint $L_{c} \ge L(q,u)$ is not incorporated in the min-max model.

There are many ways to incorporate this constraint in a minimax model. For instance, consider this model:

$$ \min_{q\in \mathit{Q}}\max_{u\in \mathscr{U}(\alpha^{*}, \widetilde{u})} \big\{L(q,u): L_{c}\ge L(q,u)\ , \ \forall u\in \mathscr{U}(\alpha_{m}, \widetilde{u}) \big\} $$

where $\alpha^{*}>>\alpha_{m}$ is the size of a neighborhood that contains $\mathscr{U}(\alpha, \widetilde{u})$ that is of special interest to the 'owner' of the problem. In fact, there could have been many other possible options for the minimax modeler. For instance, how about this model of global robustness (with respect to the objective function): $$ \min_{q\in \mathit{Q}}\max_{u\in \mathscr{U}(\color{red}\infty, \widetilde{u})} \big\{L(q,u)-g(u): L_{c}\ge L(q,u)\ , \ \forall u\in \mathscr{U}(\alpha_{m}, \widetilde{u}) \big\} $$

where $g$ is a bench mark loss function relative to which actual losses are assessed. Note that $\mathscr{U}(\color{red}\infty,\widetilde{u})$ denotes the largest neighborhood around $\widetilde{u}$ under consideration, namely is the entire uncertainty space. The difference $L(q,u)-g(u)$ can be regarded as a 'regret' a la Savage's (1951) famous minimax regret model.

In any case, it is important to note that the way the problem is described in the article, it is not clear what kind of robustness is actually required by the (incomplete) problem formulation: perhaps the uncertainty is deep, and the point estimate $\widetilde{u}$ is just a wild guess, in which case local robustness measures will not be suitable here.

In short, the article seems to be completely oblivious to the following inconvenient:

Fact: 
The two models shown in (Two Models) are representations of two different decision-making problems, and therefore it is not surprising at all that they are quite different from each other. However, both models are members of Wald's Maximin/Minimax paradigm: one model is a simple minimax model and the other (that is, the robust-satisficing decision model) is a simple maximin model.

In conclusion, rather than clarifying the relation between Wald's Maximin paradigm and IGDT, the article achieves the opposite: it adds to the confusion and misconceptions already existing in the IGDT literature regarding this relation, and the role and place of IGDT in the state of the art in decision-making under uncertainty.

Some basic misconceptions about Wald's Maximin paradigm in the IGDT literature

The IGDT literature is filled with misconceptions and erroneous statements regarding Wald's maximin paradigm, its capabilities and limitations. Some are technical, others are conceptual in nature, but most are just repeats of statements made by other scholars. I invite the interested reader to reader the reviews of dozens of IGDT related publications to see for themselves how such misconceptions are spread under the watching eyes and scrutiny of the revered peer-review process.

Before examining the relevant material in the CHAPTER, let us examine briefly old claims (called Myths below) that illustrate well why one has to be very careful with some of the rhetoric in the IGDT literature. It should be stressed that these claims are not accidental. The technical claims serve as a "proof" that IGDT core robustness related models are not maximin models. Let us see how this scheme works.

Myth 1: IGDT is radically different from all conventional methods/theories for dealing with decision making problems under uncertainty. In the two editions of the main text on IGDT, we read this:

Info-gap decision theory is radically different from all current theories of decision under uncertainty. The difference originates in the modeling of uncertainty as an information gap rather than as a probability. The need for info-gap modeling and management of uncertainty arises in dealing with severe lack of information and highly unstructured uncertainty.
Ben-Haim (2001, 2006, p. xii)

Fact 1: IGDT's two robustness related core models are Maximin models. Furthermore, IGDT's robustness is a reinvention of the well known concept radius of stability (circa 1962). Similarly, IGDT's two opportuneness related core models are Minimin models, and IGDT's opportuneness is a reinvention of the well established concept radius of instability.

Myth 2: IGDT's robustness analysis is not a worst case analysis. For example, consider this strong statement which is quite representative of the early IGDT literature

Optimization of the robustness in eq. (3.172) is emphatically not a worst-case analysis.
Ben-Haim (2006, p. 101)
And even later:
Info-gap theory is not a worst-case analysis. While there may be a worst case, one cannot know what it is and one should not base one's policy upon guesses of what it might be. Info-gap theory is related to robust-control and min-max methods, but nonetheless different from them.
Ben-Haim (2010, p. 9)

Fact 2: IGDT's robustness analysis is most definitely a worst-case analysis. In fact, in the CHAPTER we read this:

The IG robust-satisficing approach requires the planner to think in terms of the worst consequence that can be tolerated, and to choose the decision whose outcome is no worse than this, over the widest possible range of contingencies.
Ben-Haim (2019, p. 96)

Myth 3: There is no worst-case if the uncertainty is unbounded. The "proof" relies on this erroneous argument

But an info-gap model of uncertainty is an unbounded family of nested sets: $\mathscr{U}(\alpha,\widetilde{u})$, for all $\alpha \ge 0$. Consequently, there usually is no worst case: any adverse occurrence is less damaging than some other event occurring at some other extreme event occurring at a larger horizon of uncertainty $\alpha$.
Ben-Haim (2019, p. 96)

Fact 3: Not only that this claim is technically wrong, it in effect ignores the old and very respected field of unconstrained optimization where worst and best cases are sought over unbounded sets. Observe, for example, that each of the beloved and well respected $\sin$ and $\cos$ functions possesses infinitely many best and infinitely many worst values on the (unbounded) real-line.

Myth 4: Wald's maximin paradigm requires the uncertainty space to be bounded. This is a recurring theme in the IGDT literature.

Fact 4: Wald's maximin paradigm does not require the uncertainty space to be bounded. For instance, consider the case where the uncertainty space and decision space are both equal to the real line $\mathbb{R}$, and the objective function $f$ is defined by $f(x,s)=s^{2} + sx -x^{2}$. This yields the following unbounded maximin model

$$ z^{*}:= \max_{x\in \mathbb{R}} \min_{s\in \mathbb{R}} \big\{ s^{2} + sx -x^{2}\big\}$$

This is a perfectly healthy maximin model, yielding the optimal solution $(x^{*},s^{*})=(0,0)$.

Super-Myth: IGDT's robustness related models are not maximin models.

Now, this myth is not stated explicitly. It utilizes rhetoric that is more concealing than revealing. For example, consider this text

These two concepts of robustness--min-max and info-gap--are different, motivated by different information available to the analyst. The min-max concept responds to severe uncertainty that nonetheless can be bounded. The info-gap concept responds to severe uncertainty that is unbounded or whose bound is unknown. It is not surprising that min-max and info-gap robustness analyses sometimes agree on their policy recommendations, and sometimes disagree, as has been discussed elsewhere.(40)
Ben-Haim (2012, p. 1644)

Anyway you read it, the implication is clear: Info-gap's core robustness models are not minimax models, and by further implication, they are not maximin models, either.

Super-Fact IGDT's robustness related core models are definitely maximin models, in fact very simple ones. Common prototype maximin models such as (P-Maximin) and (MP-P-Maximin) are much more powerful and versatile than IGDT's robustness related core models. By analogy, it is like comparing the concept "passenger car" to the related but much less general concept "convertible, 2 seater sports car."

So, it is not surprising at all that in the IGDT literature you find peer-reviewed publications claiming such things as this.

In a sense info gap analysis may be thought of as extended and structured sensitivity analysis of preference orderings between options. While there is a superficial similarity with minimax decision making, no fixed bounds are imposed on the set of possibilities, leading to a comprehensive search of the set of possibilities and construction of functions that describe the results of that search.
Hine and Hall (2010, pp. 16-17)
And this
IGDT offers an alternative of Wald’s maximin to quantify the confidence in realising specified aspirations but enable a balance between them as a robust-satisfying method15.
Liu et al. (2021, p. 1)

And no discussion on the myths propagated in the IGDT literature can be complete if it does not mention this one.

Super-Natural Power Myth:In some sense IGDT can be viewed as a replacement for probability theory. To wit:

Information-gap (henceforth termed ‘‘info-gap’’) theory was invented to assist decision-making when there are substantial knowledge gaps and when probabilistic models of uncertainty are unreliable (Ben-Haim, 2006). In general terms, info-gap theory seeks decisions that are most likely to achieve a minimally acceptable (satisfactory) outcome in the face of uncertainty, termed robust satisficing.
Burgman et al. (2008, p. 8)

However, if they are uncertain about this model and wish to minimize the chance of unacceptably large costs, they can calculate the robust-optimal number of surveys with equation (5).
Rout et al. (2009, p. 785)

Info-gap models are used to quantify non-probabilistic "true" (Knightian) uncertainty (Ben-Haim 2006). An info-gap model is an unbounded family of nested sets, $\mathscr{U}(\alpha,\widetilde{u})$. At any level of uncertainty $\alpha$, the set $\mathscr{U}(\alpha,\widetilde{u})$ contains possible realizations of $u$. As the horizon of uncertainty $\alpha$ gets larger, the sets $\mathscr{U}(\alpha,\widetilde{u})$ become more inclusive. The info-gap model expresses the decision maker's beliefs about uncertain variation of $u$ around $\widetilde{u}$.  
Davidovitch and Ben-Haim (2010, pp. 267-8)

Reality Check: 
According to Ben-Haim (2001, 2006, 2010), IGDT is a probability, likelihood, plausibility, chance, belief FREE theory. Hence, its robustness analysis cannot possibly rank decisions according to the likelihood, or chance that they achieve acceptable (satisfactory) outcome in the face of such an uncertainty (except for trivial cases). Furthermore, IGDT cannot possibly express the decision maker's beliefs about uncertain variation of $u$ around $\widetilde{u}$.

The interesting this is that there are warnings in the IGDT literature against such misapplications of the theory. For instance, consider this text that pre-date the official birth of IGDT :

However, unlike in a probabilistic analysis, $r$ has no connotation of likelihood. We have no rigorous basis for evaluating how likely failure may be; we simply lack the information, and to make a judgment would be deceptive and could be dangerous. There may definitely be a likelihood of failure associated with any given radial tolerance. However, the available information does not allow one to assess this likelihood with any reasonable accuracy.
Ben-Haim (1994, p. 152)

And even the main text on IGDT warns users:

In info-gap set models of uncertainty we concentrate on cluster-thinking rather than on recurrence or likelihood. Given a particular quantum of information, we ask: what is the cloud of possibilities consistent with this information? How does this cloud shrink, expand and shift as our information changes? What is the gap between what is known and what could be known. We have no recurrence information, and we can make no heuristic or lexical judgments of likelihood.
Ben-Haim (2006, p. 18)

Go figure!

So although IGDT prides itself for being a probability, likelihood, plausibility, chance, belief FREE theory, it somehow manages to expresses the user's belief, and is capable of minimizing the 'chance' of unacceptable large costs. It seems that by creating measures of "likelihood' and "chance", and "belief" from nowhere, we are back to the good old days of applied alchemy.

This apparent paradox/contradiction did not go unnoticed. I raised it in writing numerous times starting in 2006, and others soon followed. For example, in a 2009 report prepared for the Department for Environment Food and Rural Affairs (UK Government), we read

More recently, Info-Gap approaches that purport to be non-probabilistic in nature developed by Ben-Haim (2006) have been applied to flood risk management by Hall and Harvey (2009). Sniedovich (2007) is critical of such approaches as they adopt a single description of the future and assume alternative futures become increasingly unlikely as they diverge from this initial description. The method therefore assumes that the most likely future system state is known a priori. Given that the system state is subject to severe uncertainty, an approach that relies on this assumption as its basis appears paradoxical, and this is strongly questioned by Sniedovich (2007).
Bramley et al. (2009, 75 )

And in a 2013 comprehensive study of IGDT applications in ecology we read

Ecologists and managers contemplating the use of IGDT should carefully consider its strengths and weaknesses, reviewed here, and not turn to it as a default approach in situations of severe uncertainty, irrespective of how this term is defined. We identify four areas of concern for IGDT in practice: sensitivity to initial estimates, localized nature of the analysis, arbitrary error model parameterisation and the ad hoc introduction of notions of plausibility."
Hayes et al. (2013, p. 1)

Sniedovich (2008) bases his arguments on mathematical proofs that may not be accessible to many ecologists but the impact of his analysis is profound. It states that IGDT provides no protection against severe uncertainty and that the use of the method to provide this protection is therefore invalid.
Hayes et al. (2013, p. 2)

The literature and discussion presented in this paper demonstrate that the results of Ben-Haim (2006) are not uncontested. Mathematical work by Sniedovich (2008, 2010a) identifies significant limitations to the analysis. Our analysis highlights a number of other important practical problems that can arise. It is important that future applications of the technique do not simply claim that it deals with severe and unbounded uncertainty but provide logical arguments addressing why the technique would be expected to provide insightful solutions in their particular situation.
Hayes et al. (2013, p. 9)

Plausibility is being evoked within IGDT in an ad hoc manner, and it is incompatible with the theory's core premise, hence any subsequent claims about the wisdom of a particular analysis have no logical foundation. It is therefore difficult to see how they could survive significant scrutiny in real-world problems. In addition, cluttering the discussion of uncertainty analysis techniques with ad hoc methods should be resisted.
Hayes et al. (2013, p. 9)

In short:

IGDT is paradoxical in its treatment of severe uncertainty: the strong local orientation of its robustness/ opportuneness models are incompatible with the severity of the uncertainty that it postulates.

In view of this, one may ask:

How is it that so many analysts/scholars still seem to be oblivious to this fundamental flaw in IGDT?

Perhaps they are convinced by rhetoric in the IGDT literature about the enormous capabilities of IGDT, such as this

Probability and info-gap modelling each emerged as a struggle between rival intellectual schools. Some philosophers of science tended to evaluate the info-gap approach in terms of how it would serve physical science in place of probability. This is like asking how probability would have served scholastic demonstrative reasoning in the place of Aristotelian logic; the answer: not at all. But then, probability arose from challenges different from those faced the scholastics, just as the info-gap decision theory which we will develop in this book aims to meet new challenges.
Ben-Haim (2001 and 2006, p. 12)

The emergence of info-gap decision theory as a viable alternative to probabilistic methods helps to reconcile Knight’s dichotomy between risk and uncertainty. But more than that, while info-gap models of severe lack of information serve to quantify Knight's 'unmeasurable uncertainty', they also provide new insight into risk, gambling, and the entire pantheon of classical probabilistic explanations. We realize the full potential of the new theory when we see that it provides new ways of thinking about old problems.
Ben-Haim (2001, p. 304; 2006, p. 342)

The management of surprises is central to the “economic problem”, and info-gap theory is a response to this challenge. This book is about how to formulate and evaluate economic decisions under severe uncertainty. The book demonstrates, through numerous examples, the info-gap methodology for reliably managing uncertainty in economics policy analysis and decision making.
Ben-Haim (2010, p. x)

Perhaps.

Be it as it may, the fact remains that IGDT is continued to be portrayed as a theory for decision making under severe (deep) uncertainty, which is precisely how it is portrayed in the CHAPTER.

We are almost done, but we still have to examine following text in the CHAPTER:

    Min-max or worst-case analysis is a widely used alternative to outcome optimization when facing deep uncertainty and bears some similarity to IG robustness. Neither min-max nor IG presumes knowledge of probabilities. The basic approach behind these two methods is to find decisions that are robust to a range of different contingencies. Wald (1947) presented the modern formulation of min-max, and it has been applied in many areas (e.g., Hansen and Sargent 2008). The decision maker considers a bounded family of possible models, without assigning probabilities to their occurrence. One then identifies the model in that set which, if true, would result in a worse outcome than any other model in the family. A decision is made that minimizes this maximally bad outcome (hence "min-max"). Min-max is attractive because it attempts to insure against the worst anticipated outcome. However, min- max has been criticized for two main reasons. First, it may be unnecessarily costly to assume the worst case. Second, the worst usually happens rarely and therefore is poorly understood. It is unreliable (and perhaps even irresponsible) to focus the decision analysis on a poorly known event (Sims 2001).

    Min-max and IG methods both deal with Knightian uncertainty, but in different ways. The min-max approach is to choose the decision for which the contingency with the worst possible outcome is as benign as possible: Identify and ameliorate the worst case. The IG robust-satisficing approach requires the planner to think in terms of the worst consequence that can be tolerated, and to choose the decision whose outcome is no worse than this, over the widest possible range of contingencies. Min-max and IG both require a prior judgment by the planner: Identify a worst model or contingency (min-max) or specify a worst tolerable outcome (IG). These prior judgments are different, and the corresponding policy selections may, or may not, agree. Ben-Haim et al. (2009) compare min-max and IG further. 
Ben-Haim (2019, p. 96)

Ask yourself this simple question:

Given that IGDT's two core robustness related models are themselves Wald-type maximin models, does the above quoted text make any sense?

To clarify: since IGDT's two robustness related models are maximin modes, any assertion on "minimax" or "maximin" in general, necessarily also applies to IGDT's robustness related models. So, among other things, the above quotes suggests that IGDT's two robustness related models are different from themselves!!!!! For example, if it is true, as claimed above, that Min-max "... bears some similarity to IG robustness ...", then the implication is that IG Robustness bears some similarities to itself! Similarly, the two main reasons that Min-max has been criticized for, must be applied also to IG robustness.

The above sweeping, general, unsubstantiated assertions about the Min-max paradigm demonstrate a lack of awareness and appreciation of the fact that Wald's Maximin/minimax paradigm offers a very wide and diverse arsenal of models, including IGDT models. There are different from each other, some more than others, but they are all members of the Maximin/Minimax family.

The reference to Ben-Haim et al. (2009) in the above quote is fascinating, and deserves attention. One of its section is dedicated to a comparison of IGDT's robust-satisficing decision model and a minimax model. For instance, consider these interesting claims:

In conclusion, the observational equivalence between min-maxing and robust-satisficing means that modellers can use either strategy to describe observed behavior of decision makers. In contrast, the behavioral difference means that actual decision makers will not necessarily be indifferent between these strategies, and will choose a strategy according to their beliefs and aspirations.
Ben-Haim et al. (2009, p. 1062)

The observational equivalence of min-maxing and robust-satisficing asserts that either can be used as a mathematical representation of the other. The behavioral difference between these methods asserts that real decision makers with specific beliefs and requirements need not be indifferent between these methods.
Ben-Haim et al. (2009, p. 1062)

Some readers may wish to read a review of this article. In any case, the question is this:

How do you response to such incoherent and unsubstantiated claims?

Good question. Here is my answer.

Given that Ben-Haim et al. (2009) claim that apparently IGDT can be used as a mathematical representation of Wald's maximin paradigm, I pose here and now the following simple challenge to the IGDT scholars who made these claims, as well as to other scholars who concur with them.

Challenge Project:

Use IGDT's robustness model or IGDT's robust-satisficing decision model to represent the following simple Wald-type maximin model:
Challenge Problem No. 1:    $\displaystyle z^{*}:= \max_{x\in \mathbb{R}^{3}} \min_{s\in S(x)} \left\{3x_{1}s_{1} + 4x_{2}s_{3} + 5x_{3}s_{2}: \sum_{j=1}^{3}(x_{j}-s_{j} )^{2} \le 100, \forall s\in S(x), x\ge \mathbf{0}\right\} $
where $ S(x) = \text{ a given convex subset of $\mathbb{R}^{3}$ that may depend on $x\in \mathbb{R}^{3}$}$.

Alternatively, formulate an IGDT representation of this very popular robust-counterpart linear programming problem:
Challenge Problem No. 2:    $\displaystyle z^{*} := \max_{x}\min_{(c,A,b)\in \mathscr{U}} \left\{ c^{T}x: Ax \le b\ , \ \forall (c,A,b)\in \mathscr{U}\right\} $
where $c, b,$ and $A$ are uncertain arrays of appropriate (matching) dimensions and $\mathscr{U}$ is the uncertainty set of these parameters under consideration. See Ben-Tal et al.'s (2009) book Robust Optimization for details on maximin/minimax models of this type.

Note that the above claims in Ben-Haim et al. (2009) imply that the entire counter-part robustness approach to uncertain mathematical programming problems can be represented by IGDT's robustness related models. This is absolutely amazing!

And if you combine the 2019 claims and the 2009 claims, you conclude that IGDT's robustness related models are actually much more powerful than Wald's maximin paradigm, as the claims imply that the former can represent situations that the latter can't!

Unfortunately, absurd claims like these still find their way to peer-reviewed publications.

I better stop here.

Summary and conclusions

As a decision theory, IGDT is fundamentally flawed, as its robustness model is incompatible with the severity of the uncertainty that it stipulates, hence it does not properly address the problem it is designed to deal with. The idea that a local robustness analysis of the radius of stability type, in the neighborhood of a guess that can be substantially wrong, is a proper way to measure robustness against uncertainty that is probability, likelihood, plausibility, chance, belief, Free, should be rejected immediately. This approach to robustness has been used properly for decades in many fields to measure the robustness/stability against small perturbation in a nominal value of a parameter. But it has no place in a theory addressing deep uncertainties, where

In fact, this ill-conceived idea should be used as an example illustrating of how not to deal with severe uncertainties of this type.

In a nutshell:

IGDT's secret weapon for dealing with deep uncertainty: 
Ignore the severity of the uncertainty! Conduct a local analysis in the neighborhood of a poor estimate that may be substantially wrong, perhaps even just a wild guess. This magic recipe works particularly well in cases where the uncertainty is unbounded! 
The obvious flaws in the recipe should not bother you, and definitely should not prevent you from claiming that the method is reliable! To wit (color is used for emphasis):
The management of surprises is central to the “economic problem”, and info-gap theory is a response to this challenge. This book is about how to formulate and evaluate economic decisions under severe uncertainty. The book demonstrates, through numerous examples, the info-gap methodology for reliably managing uncertainty in economic policy analysis and decision making.
Ben-Haim (2010, p. x)

It is time for the literature promoting the use of IGDT as a tool for decision-making under deep uncertainty to face reality, and deal with the documented criticisms that have been directed at IGDT since 2006 (perhaps even earlier), regarding its role and place in decision making under severe uncertainty. The following facts should serve as good starting points:

In the meantime, users of IGDT should be aware of the following facts:

  • Wald's maximin paradigm offers a much richer and more powerful environment for the treatment of decision-making problems than IGDT. Anything that IGDT's robustness related models can do, maximin/minimax models can do, and more! Much more!
  • Contrary to the rhetoric in the IGDT literature about the theory's role and place in the state of the art in decision-making under deep uncertainty, the theory is not suitable for the treatment of severe uncertainties of the type it postulates.
  • The CHAPTER requires a deep reality check.

Bibliography and links

Articles/chapters

Research Reports

Links