Local weather  
Brought to you by
 IF - IG 
International Interdisciplinary Center For
Information and Fact Checking about
Info-Gap Decision Theory

Local time
Home About News IGDT The Campaign Myths & Facts Reviews FAQs FUQs Resources Contact Us
The rise and rise of voodoo decision making

Reviews of publications on Info-Gap decision theory (IGDT)

Review 4-2022 (Posted: January 28, 2022; Last update: January 28, 2022)

Reference Muriel C. Bonjean Stanton, and Katy Roelich. Decision making under deep uncertainties: A review of the applicability of methods in practice. Technological Forecasting & Social Change 171, 120939
Year of publication2021
Publication typePeer-reviewed journal article.
Downloads https://doi.org/10.1016/j.techfore.2021.120939 open access.
Abstract Deep uncertainties like environmental and socio-economic changes create challenges to decision making. Decision Making under Deep Uncertainty (DMDU) methods are recognised approaches to navigate deep uncertainties and support robust and adaptable decisions. However, their ability to fully reflect the context in which these decisions are made has been criticised. This paper presents a synthesis across cases and methods to provide a holistic understanding of the application of DMDU methods to support long-term decision making. We carried out a structured literature review and analysed 37 infrastructure DMDU case studies. The analysis shows that DMDU methods are effective at developing plans to address a range of deep uncertainties and in some cases, reflecting the institutional context of the decision. However, they largely overlook the organisational and individual contexts in which decision making happens. We argue that the use of existing DMDU methods in practice should start with a better understanding of the institutional, organisational and individual contexts. We then suggest modifications to the applications of DMDU methods, i.e. internalising the context at different stages of the decision-making process and developing a decision typology to signpost decision makers to the best approach for a specific context.
ReviewerMoshe Sniedovich
IF-IG perspective This article is an excellent illustration of how a fundamentally flawed theory succeeds in getting the attention of unsuspected readers. Go figure!

The purpose of this short review is to discuss briefly the following text in the article describing IGDT.

Info-Gap Theory (IG) identifies management options that perform acceptably well under a wide range of conditions; seeking robustness rather than optimality in a process known as robust-satisficing (Ben- Haim, 2010). A strategy of satisficing robustness can be described as one that will satisfy the minimum performance requirements (performing adequately rather than optimally) over a wide range of potential scenarios even under future conditions that deviate from the best estimate (Ben-Haim, 2001).
Bonjean Stanton and Roelich (2021, p. 3)

Note that this statement gives no indication that IGDT's robustness analysis is inherently local in nature and therefore is unsuitable for the treatment of severe (deep) uncertainties of the type postulated in Ben-Haim (2001, 2006, 2010).

In any case, the issue is this

It is not clear at all on what grounds it is claimed (explicitly or implicitly) in the article that IGDT is a proper theory for the treatment of deep (severe) uncertainty. To justify the use of IGDT we must be confident that the true (but unknown) value of the uncertainty parameter is in the neighborhood of the given nominal value (guess) of the uncertainty parameter. Therefore:
  • Under deep uncertainty we most definitely lack this confidence, hence we cannot justify the use of IGDT to deal with the uncertainty under consideration.

  • If we have this confidence, then the uncertainty under consideration is definitely not deep.

No amount of rhetoric can invalidate these obvious conclusions.

And for a second opinion, they may also wish to consult the article Severe uncertainty and info-gap decision theory (Hayes et al. 2013) where they will find these assessments (colors are used for emphasis):

Ecologists and managers contemplating the use of IGDT should carefully consider its strengths and weaknesses, reviewed here, and not turn to it as a default approach in situations of severe uncertainty, irrespective of how this term is defined. We identify four areas of concern for IGDT in practice: sensitivity to initial estimates, localized nature of the analysis, arbitrary error model parameterisation and the ad hoc introduction of notions of plausibility.
Hayes et al. (2013, p. 1)

Sniedovich (2008) bases his arguments on mathematical proofs that may not be accessible to many ecologists but the impact of his analysis is profound. It states that IGDT provides no protection against severe uncertainty and that the use of the method to provide this protection is therefore invalid.
Hayes et al. (2013, p. 2)

The literature and discussion presented in this paper demonstrate that the results of Ben-Haim (2006) are not uncontested. Mathematical work by Sniedovich (2008, 2010a) identifies significant limitations to the analysis. Our analysis highlights a number of other important practical problems that can arise. It is important that future applications of the technique do not simply claim that it deals with severe and unbounded uncertainty but provide logical arguments addressing why the technique would be expected to provide insightful solutions in their particular situation.
Hayes et al. (2013, p. 9)

Plausibility is being evoked within IGDT in an ad hoc manner, and it is incompatible with the theory's core premise, hence any subsequent claims about the wisdom of a particular analysis have no logical foundation. It is therefore difficult to see how they could survive significant scrutiny in real-world problems. In addition, cluttering the discussion of uncertainty analysis techniques with ad hoc methods should be resisted.
Hayes et al. (2013, p. 609)

For the benefit of readers who are not familiar with the "local issue", here is a picture of the `paradox'. To interpret this picture correctly, it should be pointed out that according to Ben-Haim (2001, 2006, 2010) the severity of the uncertainty that the theory is designed to handle is characterized by these three features:

In this picture, the black rectangle represents the uncertainty space and the small yellow square represents the largest neighborhood around the point estimate over which a decision satisfies the performance constraint. Very close to the boundary of the square, in the black area, there is a point where the decision violates the constraint. Therefore, it is impossible to increase the size of the small square (in all directions) without violating the constrains. Hence, the size of the small square is the radius of stability (IGDT robustness) of the decision under consideration.

We have no idea how well/badly the decision performs over the large black area. Indeed, IGDT makes no attempt to explore the black area to determine how well/badly the decision performs in areas that are at a distance from the small yellow square. Clearly therefore, IGDT's measure of robustness is a measure of local robustness. For obvious reasons, such a measure of robustness is not suitable for the treatment of deep uncertainty.

One of the challenges posed by deep uncertainty is the need to explore a vast and diverse uncertainty space to determine how well/badly decisions perform over this space. Note that IGDT prides itself for being able to cope with unbounded uncertainty spaces. In such cases, the small yellow square will be infinitesimally small compared to the black area. I refer to the black area as the No-man's Land of IGDT's robustness analysis.

For the benefit of readers who are not familiar with the concept "radius of stability" (= "stability radius"), here is a list of quotes.

The formulae of the last chapter will hold only up to a certain "radius of stability," beyond which the stars are swept away by external forces.
von Hoerner (1957, p. 460)

It is convenient to use the term "radius of stability of a formula" for the radius of the largest circle with center at the origin in the s-plane inside which the formula remains stable.
Milner and Reynolds (1962, p. 67)

The radius $r$ of the sphere is termed the radius of stability (see [33]). Knowledge of this radius is important, because it tells us how far one can uniformly strain the (engineering, economic) system before it begins to break down.
Zlobec (1987, p. 326)

An important concept in the study of regions of stability is the "radius of stability" (e.g., [65, 89]). This is the radius $r$ of the largest open sphere $S(\theta^{*}, r)$, centered at $\theta^{*}$, with the property that the model is stable, at every point $\theta$ in $S(\theta^{*}, r)$. Knowledge of this radius is important, because it tells us how far one can uniformly strain the system before it begins to "break down". (In an electrical power system, the latter may manifest in a sudden loss of power, or a short circuit, due to a too high consumer demand for energy. Our approach to optimality, via regions of stability, may also help understand the puzzling phenomenon of voltage collapse in electrical networks described, e.g., in [11].)
Zlobec (1988, p. 129)

Robustness, or insensitivity to perturbations, is an essential property of a control-system design. In frequency-response analysis the concept of stability margin has long been in use as a measure of the size of plant disturbances or model uncertainties that can be tolerated before a system loses stability. Recently a state-space approach has been established for measuring the "distance to instability" or "stability radiusā€¯ of a linear multivariable system, and numerical methods for computing this measure have been derived [2,7,8,11].
Byers and Nichols (1993, pp. 113-114)

Robustness analysis has played a prominent role in the theory of linear systems. In particular the state-state approach via stability radii has received considerable attention, see [HP2], [HP3], and references therein. In this approach a perturbation structure is defined for a realization of the system, and the robustness of the system is identified with the norm of the smallest destabilizing perturbation. In recent years there has been a great deal of work done on extending these results to more general perturbation classes, see, for example, the survey paper [PD], and for recent results on stability radii with respect to real perturbations, see [QBR*].
Paice and Wirth (1998, p. 289)

The stability radius is a worst case measure of robustness. It measures the size of the smallest perturbation for which the perturbed system is either not well-posed or does not have spectrum in $\mathbb{C}_{g}$.
Hinrichsen and Prichard (2005, p. 585)

The radius of the largest ball centered at $\theta^{*}$ , with the property that the model is stable at its every interior point $\theta$, is the radius of stability at $\theta^{*}$, e. g., [69]. It is a measure of how much the system can be uniformly strained from $\theta^{*}$ before it starts breaking down.
Zlobec (2009, p. 2619)

Stability radius is defined as the smallest change to a system parameter that results in shifting eigenvalues so that the corresponding system is unstable.
Bingham and Ting (2013, p. 843)

Using stability radius to assess a system's behavior is limited to those systems that can be mathematically modeled and their equilibria determined. This restricts the analysis to local behavior determined by the fixed points of the dynamical system. Therefore, stability radius is only descriptive of the local stability and does not explain the global stability of a system.
Bingham and Ting (2013, p. 846)

Note that the discussions in Zlobec (1987, 1988, 2009) are in the context of parametric analysis of optimization problems.

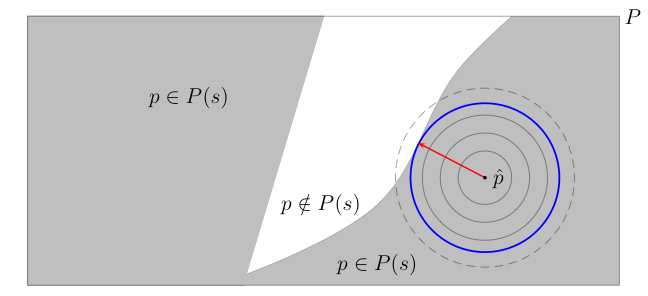
The picture is this:

Here $P$ denotes the set of values parameter $p$ can take, $P(s)$ denotes the set comprising of parameter values where the system is stable (shown in gray), and the white region represent the set of parameter values where the system is unstable. The radius of stability of the system at $\widetilde{p}$ is equal to the shortest distance from $\widetilde{p}$ to instability. It is the radius of the largest neighborhood around $\widetilde{p}$ all whose points are stable.

Clearly, this measure of robustness is inherently local in nature, as it explores the immediate neighborhood of the nominal value of the parameter, and the exploration is extended only as long as all the points in the extended neighborhood are stable. By design then, this measure does not attempt to explore the entire set of possible values of the parameter. Rather, it focuses on the immediate neighborhood of the nominal value of the parameter. The expansion of the neighborhood terminates as soon as an unstable value of the parameter is encountered. So technically, methods based on this measure of robustness, such as IGDT, are in fact based on a local worst-case analysis.

Note that under deep uncertainty the nominal value of the parameter can be substantially wrong, even just a wild guess. Furthermore, in this uncertain environment there is no guarantee that "true" value of the parameter is more likely to be in the neighborhood of the nominal value than in neighborhood of any other value of the parameter. That is, such a local analysis cannot be justified on the basis of "likelihood", or "plausibility", or "chance", or "belief" regarding the location of the true value of the parameter, simply because under deep uncertainty the quantification of the uncertainty is probability, likelihood, plausibility, chance, and belief FREE!.

And to appreciate why IGDT is fundamentally flawed, the readers may wish to read Review_2_2022.

Summary and conclusions

DMDU's Axiom of Choice:
  • If your favorite uncertainty is DEEP, don't treat it with IGDT! 
  • If your favorite decision theory is IGDT, don't apply to your DEEP uncertainty. 
Warning! If you think that IGDT treats your uncertainty properly, then ... your beloved uncertainty is not DEEP, after all!

Bibliography and links

Articles/chapters

Research Reports

Links

Disclaimer: This site, its contents and style, are the responsibility of its owner the author and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.