Local weather  
Brought to you by
 IF - IG 
International Interdisciplinary Center For
Information and Fact Checking about
Info-Gap Decision Theory

Local time
Home About News IGDT The Campaign Myths & Facts Reviews FAQs FUQs Resources Contact Us
The rise and rise of voodoo decision making

Reviews of publications on Info-Gap decision theory (IGDT)

Review 3-2022 (Posted: January 28, 2022; Last update: January 28, 2022)

Reference C. McPhail , H. R. Maier , J. H. Kwakkel , M. Giuliani , A. Castelletti , and S. Westra. (2018) Robustness Metrics: How Are They Calculated, When Should They Be Used and Why Do They Give Different Results? Earth's Future, 6, 169-191.
Year of publication2018
Publication typeOpen Source, Peer-reviewed article
Downloads https://doi.org/10.1002/2017EF000649
Abstract Robustness is being used increasingly for decision analysis in relation to deep uncertainty and many metrics have been proposed for its quantification. Recent studies have shown that the application of different robustness metrics can result in different rankings of decision alternatives, but there has been little discussion of what potential causes for this might be. To shed some light on this issue, we present a unifying framework for the calculation of robustness metrics, which assists with understanding how robustness metrics work, when they should be used, and why they sometimes disagree. The frame- work categorizes the suitability of metrics to a decision-maker based on (1) the decision-context (i.e., the suitability of using absolute performance or regret), (2) the decision-maker’s preferred level of risk aversion, and (3) the decision-maker’s preference toward maximizing performance, minimizing variance, or some higher-order moment. This article also introduces a conceptual framework describing when relative robustness values of decision alternatives obtained using different metrics are likely to agree and disagree. This is used as a measure of how “stable” the ranking of decision alternatives is when determined using different robustness metrics. The framework is tested on three case studies, including water supply augmentation in Adelaide, Australia, the operation of a multipurpose regulated lake in Italy, and flood protection for a hypothetical river based on a reach of the river Rhine in the Netherlands. The proposed conceptual framework is confirmed by the case study results, providing insight into the reasons for disagreements between rankings obtained using different robustness metrics.
ReviewerMoshe Sniedovich
IF-IG perspective Why is it so difficult for DMDU scholars to handle properly the concept "radius of stability" and to assess properly Wald's maximin paradigm?

The main purpose of this short review is to discuss briefly two issues, namely the ever-present "radius of stability" issue, and basic modeling issues pertaining to Wald's maximin paradigm.

Radius of stability

The following text explains why IGDT is not discussed in detail in the article (colors are used here for emphasis)

Satisficing metrics can also be based on the idea of a radius of stability, which has made a recent resurgence under the label of info-gap decision theory (Ben-Haim, 2004; Herman et al., 2015). Here, one identifies the uncertainty horizon over which a given decision alternative performs satisfactorily. The uncertainty horizon α is the distance from a pre-specified reference scenario to the first scenario in which the pre-specified performance threshold is no longer met (Hall et al., 2012; Korteling et al., 2012). However, as these metrics are based on deviations from an expected future scenario, they only assess robustness locally and are therefore not suited to dealing with deep uncertainty (Maier et al., 2016). These metrics also assume that the uncertainty increases at the same rate for all uncertain factors when calculating the uncertainty horizon on a set of axes. Consequently, they are shown in parentheses in Table 2 and will not be considered further in this article.
McPhail et a. (2018, p. 174).

So, the good news is that, as can be clearly seen, the main message about IGDT is getting across: IGDT is unsuitable for the treatment of severe (deep) uncertainties of the type postulated in Ben-Haim (2001, 2006, 2010) and many other publications. However, it is necessary to mention the following points regarding the treatment of the concept "radius of stability" in the article.

For the benefit of readers who are not familiar with the concept "radius of stability" (= "stability radius"), here is a list of quotes.

The formulae of the last chapter will hold only up to a certain "radius of stability," beyond which the stars are swept away by external forces.
von Hoerner (1957, p. 460)

It is convenient to use the term "radius of stability of a formula" for the radius of the largest circle with center at the origin in the s-plane inside which the formula remains stable.
Milner and Reynolds (1962, p. 67)

The radius $r$ of the sphere is termed the radius of stability (see [33]). Knowledge of this radius is important, because it tells us how far one can uniformly strain the (engineering, economic) system before it begins to break down.
Zlobec (1987, p. 326)

An important concept in the study of regions of stability is the "radius of stability" (e.g., [65, 89]). This is the radius $r$ of the largest open sphere $S(\theta^{*}, r)$, centered at $\theta^{*}$, with the property that the model is stable, at every point $\theta$ in $S(\theta^{*}, r)$. Knowledge of this radius is important, because it tells us how far one can uniformly strain the system before it begins to "break down". (In an electrical power system, the latter may manifest in a sudden loss of power, or a short circuit, due to a too high consumer demand for energy. Our approach to optimality, via regions of stability, may also help understand the puzzling phenomenon of voltage collapse in electrical networks described, e.g., in [11].)
Zlobec (1988, p. 129)

Robustness, or insensitivity to perturbations, is an essential property of a control-system design. In frequency-response analysis the concept of stability margin has long been in use as a measure of the size of plant disturbances or model uncertainties that can be tolerated before a system loses stability. Recently a state-space approach has been established for measuring the "distance to instability" or "stability radius” of a linear multivariable system, and numerical methods for computing this measure have been derived [2,7,8,11].
Byers and Nichols (1993, pp. 113-114)

Robustness analysis has played a prominent role in the theory of linear systems. In particular the state-state approach via stability radii has received considerable attention, see [HP2], [HP3], and references therein. In this approach a perturbation structure is defined for a realization of the system, and the robustness of the system is identified with the norm of the smallest destabilizing perturbation. In recent years there has been a great deal of work done on extending these results to more general perturbation classes, see, for example, the survey paper [PD], and for recent results on stability radii with respect to real perturbations, see [QBR*].
Paice and Wirth (1998, p. 289)

The stability radius is a worst case measure of robustness. It measures the size of the smallest perturbation for which the perturbed system is either not well-posed or does not have spectrum in $\mathbb{C}_{g}$.
Hinrichsen and Prichard (2005, p. 585)

The radius of the largest ball centered at $\theta^{*}$ , with the property that the model is stable at its every interior point $\theta$, is the radius of stability at $\theta^{*}$, e. g., [69]. It is a measure of how much the system can be uniformly strained from $\theta^{*}$ before it starts breaking down.
Zlobec (2009, p. 2619)

Stability radius is defined as the smallest change to a system parameter that results in shifting eigenvalues so that the corresponding system is unstable.
Bingham and Ting (2013, p. 843)

Using stability radius to assess a system's behavior is limited to those systems that can be mathematically modeled and their equilibria determined. This restricts the analysis to local behavior determined by the fixed points of the dynamical system. Therefore, stability radius is only descriptive of the local stability and does not explain the global stability of a system.
Bingham and Ting (2013, p. 846)

Note that the discussions in Zlobec (1987, 1988, 2009) are in the context of parametric analysis of optimization problems.

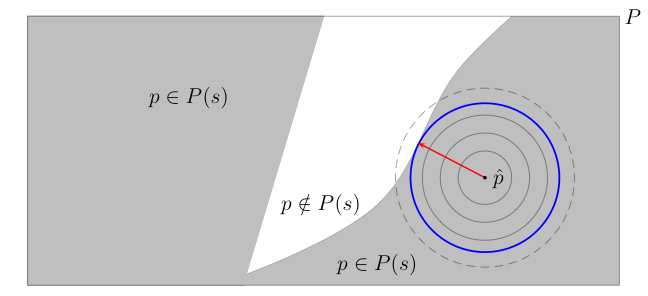
The picture is this:

Here $P$ denotes the set of values parameter $p$ can take, $P(s)$ denotes the set comprising of parameter values where the system is stable (shown in gray), and the white region represent the set of parameter values where the system is unstable. The radius of stability of the system at $\widetilde{p}$ is equal to the shortest distance from $\widetilde{p}$ to instability. It is the radius of the largest neighborhood around $\widetilde{p}$ all whose points are stable.

Clearly, this measure of robustness is inherently local in nature, as it explores the immediate neighborhood of the nominal value of the parameter, and the exploration is extended only as long as all the points in the extended neighborhood are stable. By design then, this measure does not attempt to explore the entire set of possible values of the parameter. Rather, it focuses on the immediate neighborhood of the nominal value of the parameter. The expansion of the neighborhood terminates as soon as an unstable value of the parameter is encountered. So technically, methods based on this measure of robustness, such as IGDT, are in fact based on a local worst-case analysis.

Note that under deep uncertainty the nominal value of the parameter can be substantially wrong, even just a wild guess. Furthermore, in this uncertain environment there is no guarantee that "true" value of the parameter is more likely to be in the neighborhood of the nominal value than in neighborhood of any other value of the parameter. That is, such a local analysis cannot be justified on the basis of "likelihood", or "plausibility", or "chance", or "belief" regarding the location of the true value of the parameter, simply because under deep uncertainty the quantification of the uncertainty is probability, likelihood, plausibility, chance, and belief FREE!.

In short, what emerges then is this:

IGDT's secret weapon for dealing with deep uncertainty: 
Ignore the severity of the uncertainty! Conduct a local analysis in the neighborhood of a poor estimate that may be substantially wrong, perhaps even just a wild guess. This magic recipe works particularly well in cases where the uncertainty is unbounded! 
The obvious flaws in the recipe should not bother you, and definitely should not prevent you from claiming that the method is reliable! To wit (color is used for emphasis):
The management of surprises is central to the “economic problem”, and info-gap theory is a response to this challenge. This book is about how to formulate and evaluate economic decisions under severe uncertainty. The book demonstrates, through numerous examples, the info-gap methodology for reliably managing uncertainty in economic policy analysis and decision making.
Ben-Haim (2010, p. x)

And I ask:

How can a methodology that ignores the severity of the uncertainty it is supposed to deal with possibly provide a reliable foundation for economic policy and decision making under such an uncertainty?

Wald's maximin paradigm

Since Wald's maximin paradigm is mentioned repeatedly in the article and its robustness is classified throughout the article, it is surprising that the article does not mention the fact that IGDT's robustness model and IGDT's robust-satisficing decision models are simple maximin models (see Review 2-2022). Furthermore, Table 2 assigns IGDT and maximin to different classes: IGDT is assigned to the class where there is " Indication of whether system performance is satisfactory or not" whereas maximin is assigned to the class where there is "Indication of actual system performance".

Are we to conclude from this that for some strange reason, that the article does not mention, maximin models cannot include "performance constraints"? More surprisingly, are we to conclude that IGDT's robust-satisficing decision model is not a maximin model?!

Before we examine this apparent contradiction, or inconsistency, in the proposed classification scheme, the reader is reminded that performance constraints are at the very heart of robust optimization models derived by the popular robust-counterpart approach that systematically generates maximin/minimax models from uncertain parametric optimization problems (Ben-Tal et al., 2009). And the irony is that Ben-Tal et al. (2009) is one of the references in the article!

This misclassification in the article is a manifestation of the fact that the proposed classification does not take into account the fact that there are decision making models where "performance" is measured by two factors: (1) an objective function and (2) performance constraints. Furthermore, in such models it might be possible to incorporate performance "thresholds". Hence, the same method can be classified in different ways depending on the choice of what constitutes "performance".

To illustrate this point, consider the following maximin models (see Review 2-2022 for a discussion on maximin models of these types):

$$ \begin{align} z^{*}:& = \max_{x\in X} \min_{s\in S(x)} \ f(x,s) \tag{Model 1}\\ z^{*}:& = \max_{x\in X} \min_{s\in S(x)} \ f(x,s) - t(s) \tag{Model 2}\\ z^{*}:& = \max_{x\in X} \min_{s\in (x)} \ \big\{f(x,s): g(x,s) \ge c \ , \forall s\in S(x)\big\}\tag{Model 3}\\ z^{*}:& = \max_{x\in X} \min_{s\in S(x)} \ \big\{f(x,s)-t(s): g(x,s) \ge c \ , \forall s\in S(x) \big\}\tag{Model 4}\\ z^{*}:& = \max_{x\in X, q\in \mathbb{R}} \ \big\{q: q \le f(x,s), g(x,s) \ge c \ , \forall s\in S(x) \big\}\tag{Model 5}\\ z^{*}:&=\max_{x\in X,\alpha\ge 0} \big\{\alpha: g(x,u) \ge c \ , \forall u\in \mathscr{U}(\alpha,\widetilde{u}) \big\}\tag{Model 6} \end{align} $$

Here $\mathbb{R}$ denotes the real line, the objective function $f$ specifies the performance with regard to "payoffs" and $g$ specifies the performance with regard to "satisfaction" of performance constraints. In (Model 2) and (Model 4), function $t$ specifies predetermined threshold levels for the "payoffs" (for each state). Observe that (Model 6) is IGDT's robust-satisficing decision model and that maximin models such as (Model 5) are very popular in the area of robust optimization (Ben-Tal et al. 2009). They are characterized by the property that the active objective function does not depend on the state variable, hence the $\min$ operation is superfluous. Also note that (Model 5) is equivalent to (Model 3).

How would you classify these models in the framework of the classification scheme proposed in the article? And how about this maximin model?

$$ \begin{align} z^{*}:& = \max_{x\in X} \min_{s\in S''(x)} \ \big\{g(x,s)-t(s): g(x,u) \ge c \ , \forall s\in S'(x) \big\}\tag{Model 7}\\ \end{align} $$ where say $S'(x)$ is a small subset of $S''$.

In summary: the classification proposed in the article requires some refinements and/or modifications, as it clearly cannot handle properly the maximin paradigm. In Table 2 it assigns the generic "maximin" paradigm to one class and one of its instances (IGDT's robust-satisficing decision model) to another class. I haven't checked the proposed classification scheme in detail. There might be other contradictions/inconsistencies in the methodology. Or perhaps the difficulty actually lies in lack of awareness and appreciation of the modeling aspects of Wald's maximin paradigm that is so prevalent in the IGDT and DMUDU literature.

Historical perspective

Hard as I tried, I cannot figure out the historical perspective given in the article to the development of metrics of robustness for system performance under deep uncertainty. Consider this statement (color is used for emphasis):

It should be noted that while robustness metrics have been considered in different problem domains, such as water resources planning (Hashimoto et al., 1982b), dynamic chemical reaction models (Samsatli et al., 1998), timetable scheduling (Canon & Jeannot, 2007), and data center network service levels (Bilal et al., 2013) for some time, this has generally been in the context of perturbations centered on expected conditions, or local uncertainty, rather than deep uncertainty. In contrast, consideration of robustness metrics for quantifying system performance under deep uncertainty, which is the focus of this article, has only occurred relatively recently.
McPhail et al. (2019, p. 170)

The question is how "recently"? The answer is given in the next paragraph following immediately the above quote:

A number of robustness metrics have been used to measure system performance under deep uncertainty, such as:
  • Expected value metrics (Wald, 1950), which indicate an expected level of performance across a range of scenarios.
  • Metrics of higher-order moments, such as variance and skew (e.g., Kwakkel et al., 2016b), which provide information on how the expected level of performance varies across multiple scenarios.
  • Regret-based metrics (Savage, 1951), where the regret of a decision alternative is defined as the difference between the performance of the selected option for a particular plausible condition and the performance of the best possible option for that condition.
  • Satisficing metrics (Simon, 1956), which calculate the range of scenarios that have acceptable performance relative to a threshold.
McPhail et al. (2019, p. 170)

So we are back to the 1950s! Indeed, if you examine Table 1 A Summary of the Three Transformations that are Used by Each Robustness Metric Considered in This Article, you discover that 7 of the 11 metrics considered in the article are old timers!

In fact, you'll also discover that Table 1 is missing a very popular and active method that is definitely relatively recent, and that is very relevant to this article: Robust Optimization. Interestingly, the substantive discussion in the article does not mention this popular method/approach. In contrast, this method features in the title of 4 references.

I better stop right here.

Summary and conclusions

The continued mishandling in the DMDU literature of the IGDT-Radius of stability connection is not healthy and should be resolved, the sooner the better. This literature should also address the IGDT vs Wald's maximin connection.

Attempts to classify robustness metrics for decision making under severe uncertainty should be aware and appreciate the modeling power and versatility of Wald's maximin paradigm, hence of the robust-counterpart method of Robust Optimization that transforms uncertain parametric constrained optimization problems into maximin/minimax problems.

Bibliography and links

Articles/chapters

Research Reports

Links

Disclaimer: This site, its contents and style, are the responsibility of its owner the author and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.