Local weather  
Brought to you by
 IF - IG 
International Interdisciplinary Center For
Information and Fact Checking about
Info-Gap Decision Theory

Local time
Home About News IGDT The Campaign Myths & Facts Reviews FAQs FUQs Resources Contact Us
The rise and rise of voodoo decision making

Reviews of publications on Info-Gap decision theory (IGDT)

Review 1-2022 (Posted: January 28, 2022; Last update: January 28, 2022)

Reference Vincent A. W. J. Marchau, Warren E. Walker, Pieter J. T. M. Bloemen, and Steven W. Popper (Editors) Decision Making under Deep Uncertainty. Springer.
Year of publication2019
Publication typeEdited open access book
Downloads Publisher's website (Freely accessible PDF files, by chapter)
Two paragraphs from the Preface Several books have been written in the past that deal with different aspects of decisionmaking under uncertainty (in a broad sense). But, there are none that aim to integrate these aspects for the specific subset of decisionmaking under deep uncertainty. This book provides a unified and comprehensive treatment of the approaches and tools for developing policies under deep uncertainty, and their application. It elucidates the state of the art in both theory and practice associated with the approaches and tools for decisionmaking under deep uncertainty. It has been produced under the aegis of the Society for Decision Making under Deep Uncertainty (DMDU: http://www.deepuncertainty.org), whose members develop the approaches and tools supporting the design of courses of action or policies under deep uncertainty, and work to apply them in the real world.
Page v      

The book provides the first synthesis of the large body of work on designing policies under deep uncertainty, in both theory and practice. It broadens traditional approaches and tools to include the analysis of actors and networks related to the problem at hand. And it shows how lessons learned in the application process can be used to improve the approaches and tools used in the design process.
Page vi     
ReviewerMoshe Sniedovich
Public Disclosure: 
To the best of my knowledge, the "local issue", the "maximin issue", as well as other issues, were first raised in writing in 2006, in the report What's wrong with info-gap? An Operations Research Perspective that was posted on my old website at Uni. The first peer-reviewed article on these "issues" was published in 2007 (see bibliography below). The Father of IGDT, Prof. Yakov Ben-Haim, is familiar with my criticism of his theory. Indeed, in 2007 he attended two of my lectures where I discussed in detail the major flaws in IGDT.
IF-IG perspective This book is an excellent illustration of how a fundamentally flawed theory, such as IGDT, succeeds in getting the attention of unsuspected readers. Here, a book dedicated to decision making under DEEP uncertainty tells us, albeit in a somewhat cryptic manner, that a model of local robustness, specifically a radius of stability type model, is an appropriate tool for the treatment of Deep uncertainty. The book also includes two chapters on IGDT. The implication thus must be that the book regards IGDT as a suitable decision theory for the treatment of deep uncertainty. Therefore, the book is reviewed with this in mind.

The book consists of 17 chapters grouped into 4 parts:

  1. Introduction, by Marchau, Walker, Bloemen and Popper. 
    Part I DMDU Approaches
  2. Robust Decision Making (RDM), by Lempert.
  3. Dynamic Adaptive Planning (DAP) by Walker, Marchau and Kwakkel.
  4. Dynamic Adaptive Policy Pathways (DAPP) by Haasnoot, Warren and Kwakkel.
  5. Info-Gap Decision Theory (IG) by Ben-Haim.
  6. Engineering Options Analysis (EOA) by de Neufville and Smet. 
    Part II DMDU Applications
  7. Robust Decision Making (RDM): Application to Water Planning and Climate Policy, Groves, Molina-Perez, Bloom and Fischbach.
  8. Dynamic Adaptive Planning (DAP): The Case of Intelligent Speed Adaptation by Marchau, Walker and van der Pas.
  9. Dynamic Adaptive Policy Pathways (DAPP): From Theory to Practice by Lawrence, Haasnoot, McKim, Atapattu, Campbell and Stroombergen,
  10. Info-Gap (IG): Robust Design of a Mechanical Latch, by Hemez and Van Buren.
  11. Engineering Options Analysis (EOA): Applications by de Neufville, Smet, Cardin and Ranjbar-Bourani. 
    Part III DMDU-Implementation Processes
  12. Decision Scaling (DS): Decision Support for Climate Change, byBrown, Steinschneider, Ray, Wi, Basdekas and Yates
  13. A Conceptual Model of Planned Adaptation (PA), by Sowell
  14. DMDU into Practice: Adaptive Delta Management inThe Netherlands, by Bloemen, Hammer, van der Vlist, Grinwis and van Alphen. 
    Part IV DMDU-Synthesis
  15. Supporting DMDU: A Taxonomy of Approaches and Tools, by Kwakkel and Haasnoot.
  16. Reflections: DMDU and Public Policy for Uncertain Times, by Popper.
  17. Conclusions and Outlook, Marchau, Walker, Bloemen and Popper.

From the Glossary:

Deep uncertainty ‘The condition in which analysts do not know or the parties to a decision cannot agree upon (1) the appropriate models to describe inter- actions among a system’s variables, (2) the probability distributions to represent uncertainty about key parameters in the models, and/or (3) how to value the desirability of alternative outcomes’ (Lempert et al. 2003). In this book, deep uncertainty is seen as the highest of four defined levels of uncertainty.
p. 402          

Robust Policy A robust policy can keep on meeting the desired objectives as new information becomes available or as the situation changes.
p. 404          

At the moment, my plan is to review

The review of Chapter 5 has already been posted, and I plan to complete the reviews of the other chapters within a month or two, or three.

In this review I briefly discuss the book from an IF-IG perspective, hence focusing on the two chapters on IGDT. I may modify it if necessary later on after I complete the reviews of the four chapters listed above.

According to the Preface and Introduction, the book is supposed to provide information on the state of the art in decision making under deep uncertainty. Furthermore, the coverage of each approach should provide the "... latest methodological insights, and challenges for improvement ..." (see page 17). Unfortunately, as far as IGDT is concerned, what we find in the book on this theory, especially in Chapter 5, is mainly the same old unsubstantiated rhetoric. I have to read Chapter 10 once more to try to find some trace of deep uncertainty there.

In short, the book does not deal at all with the well document criticisms of IGDT and the rhetoric about it, that can be summarized as follows:

  • IGDT's robustness and opportuneness analyses are both inherently local in nature. 
  • Therefore, IGDT is not suitable for the treatment of severe (deep) uncertainties of the type it postulates. 
  • IGDT's flagship concept, namely the concept "Info-gap robustness" is a reinvention of the well known concept Radius of Stability (circa 1960). 
  • IGDT's robustness model and IGDT's robust-satisficing decision model are simple Wald-Type maximin models (circa 1940). 
  • IGDT's opportuneness and IGDT's opportune-satisficing decision models are simple Minimin models, hence conventional constrained minimization models.  
  • The IGDT literature spreads misconceptions and unsubstantiated claims about IGDT's role and place in the state of the art in decision making under severe (deep) uncertainty.

All these points are discussed in detail in the review of Chapter 5 so I discuss them here only briefly.

Interestingly, here is a short, but informative, explanation of why IGDT is not included in the list of robustness metrics analyzed in the article Robustness Metrics: How Are They Calculated, When Should They Be Used and Why Do They Give Different Results? (McPhail et al. 2018) (colors are added for emphasis):

Satisficing metrics can also be based on the idea of a radius of stability, which has made a recent resurgence under the label of info-gap decision theory (Ben-Haim, 2004; Herman et al., 2015). Here, one identifies the uncertainty horizon over which a given decision alternative performs satisfactorily. The uncertainty horizon $\alpha$ is the distance from a pre-specified reference scenario to the first scenario in which the pre-specified performance threshold is no longer met (Hall et al., 2012; Korteling et al., 2012). However, as these metrics are based on deviations from an expected future scenario, they only assess robustness locally and are therefore not suited to dealing with deep uncertainty (Maier et al., 2016). These metrics also assume that the uncertainty increases at the same rate for all uncertain factors when calculating the uncertainty horizon on a set of axes. Consequently, they are shown in parentheses in Table 2 and will not be considered further in this article.
McPhail et al. (2018, p. 174)

And here are some comments on why local robustness analyses are not compatible with deep uncertainty:

As pointed out by Maier et al. (2016), when dealing with deep uncertainty, system performance is generally measured using metrics that preference systems that perform well under a range of plausible conditions, which fall under the umbrella of robustness. It should be noted that while robustness metrics have been considered in different problem domains, such as water resources planning (Hashimoto et al., 1982b), dynamic chemical reaction models (Samsatli et al., 1998), timetable scheduling (Canon & Jeannot, 2007), and data center network service levels (Bilal et al., 2013) for some time, this has generally been in the context of perturbations centered on expected conditions, or local uncertainty, rather than deep uncertainty. In contrast, consideration of robustness metrics for quantifying system performance under deep uncertainty, which is the focus of this article, has only occurred relatively recently.
McPhail et al. (2018, p. 170)

In sharp contrast, although the book is definitely aware of the inherent local orientation of IGDT, it nevertheless presents IGDT as a decision theory for the treatment of deep uncertainty: two chapters in the book are dedicated to this theory (color is added for emphasis).

Info-Gap Decision Theory (IG): An information gap is defined as the disparity between what is known and what needs to be known in order to make a reliable and responsible decision. IG is a non-probabilistic decision theory that seeks to optimize robustness to failure (or opportunity for windfall) under deep uncertainty. It starts with a set of alternative actions and evaluates the actions computationally (using a local robustness model). It can, therefore, be considered as a computational support tool, although it could also be categorized as an approach for robust decisionmaking (Ben-Haim 1999).
Chapter 1, p. 16

Interestingly, both Chapter 5 and Chapter 10 are totally oblivious to the "local" issue.

For the benefit of readers who are not familiar with the "local issue", here is a picture of the `paradox'. To interpret this picture correctly, it should be pointed out that according to Ben-Haim (2001, 2006, 2010) the severity of the uncertainty that the theory is designed to handle is characterized by these three features:

In this picture, the black rectangle represents the uncertainty space and the small yellow square represents the largest neighborhood around the point estimate over which a decision satisfies the performance constraint. Very close to the boundary of the square, in the black area, there is a point where the decision violates the constraint. Therefore, it is impossible to increase the size of the small square (in all directions) without violating the constrains. Hence, the size of the small square is the radius of stability (IGDT robustness) of the decision under consideration.

We have no idea how well/badly the decision performs over the large black area. Indeed, IGDT makes no attempt to explore the black area to determine how well/badly the decision performs in areas that are at a distance from the small yellow square. Clearly therefore, IGDT's measure of robustness is a measure of local robustness. For obvious reasons, such a measure of robustness is not suitable for the treatment of deep uncertainty.

One of the challenges posed by deep uncertainty is the need to explore a vast and diverse uncertainty space to determine how well/badly decisions perform over this space. Note that IGDT prides itself for being able to cope with unbounded uncertainty spaces. In such cases, the small yellow square will be infinitesimally small compared to the black area. I refer to the black area as the No-man's Land of IGDT's robustness analysis.

For the benefit of readers who are not familiar with the concept "radius of stability" (= "stability radius"), here is a list of informative quotes.

The formulae of the last chapter will hold only up to a certain "radius of stability," beyond which the stars are swept away by external forces.
von Hoerner (1957, p. 460)

It is convenient to use the term "radius of stability of a formula" for the radius of the largest circle with center at the origin in the s-plane inside which the formula remains stable.
Milner and Reynolds (1962, p. 67)

The radius $r$ of the sphere is termed the radius of stability (see [33]). Knowledge of this radius is important, because it tells us how far one can uniformly strain the (engineering, economic) system before it begins to break down.
Zlobec (1987, p. 326)

An important concept in the study of regions of stability is the "radius of stability" (e.g., [65, 89]). This is the radius $r$ of the largest open sphere $S(\theta^{*}, r)$, centered at $\theta^{*}$, with the property that the model is stable, at every point $\theta$ in $S(\theta^{*}, r)$. Knowledge of this radius is important, because it tells us how far one can uniformly strain the system before it begins to "break down". (In an electrical power system, the latter may manifest in a sudden loss of power, or a short circuit, due to a too high consumer demand for energy. Our approach to optimality, via regions of stability, may also help understand the puzzling phenomenon of voltage collapse in electrical networks described, e.g., in [11].)
Zlobec (1988, p. 129)

Robustness, or insensitivity to perturbations, is an essential property of a control-system design. In frequency-response analysis the concept of stability margin has long been in use as a measure of the size of plant disturbances or model uncertainties that can be tolerated before a system loses stability. Recently a state-space approach has been established for measuring the "distance to instability" or "stability radius” of a linear multivariable system, and numerical methods for computing this measure have been derived [2,7,8,11].
Byers and Nichols (1993, pp. 113-114)

Robustness analysis has played a prominent role in the theory of linear systems. In particular the state-state approach via stability radii has received considerable attention, see [HP2], [HP3], and references therein. In this approach a perturbation structure is defined for a realization of the system, and the robustness of the system is identified with the norm of the smallest destabilizing perturbation. In recent years there has been a great deal of work done on extending these results to more general perturbation classes, see, for example, the survey paper [PD], and for recent results on stability radii with respect to real perturbations, see [QBR*].
Paice and Wirth (1998, p. 289)

The stability radius is a worst case measure of robustness. It measures the size of the smallest perturbation for which the perturbed system is either not well-posed or does not have spectrum in $\mathbb{C}_{g}$.
Hinrichsen and Prichard (2005, p. 585)

The radius of the largest ball centered at $\theta^{*}$ , with the property that the model is stable at its every interior point $\theta$, is the radius of stability at $\theta^{*}$, e. g., [69]. It is a measure of how much the system can be uniformly strained from $\theta^{*}$ before it starts breaking down.
Zlobec (2009, p. 2619)

Stability radius is defined as the smallest change to a system parameter that results in shifting eigenvalues so that the corresponding system is unstable.
Bingham and Ting (2013, p. 843)

Using stability radius to assess a system's behavior is limited to those systems that can be mathematically modeled and their equilibria determined. This restricts the analysis to local behavior determined by the fixed points of the dynamical system. Therefore, stability radius is only descriptive of the local stability and does not explain the global stability of a system.
Bingham and Ting (2013, p. 846)

Note that the discussions in Zlobec (1987, 1988, 2009) are in the context of parametric analysis of optimization problems.

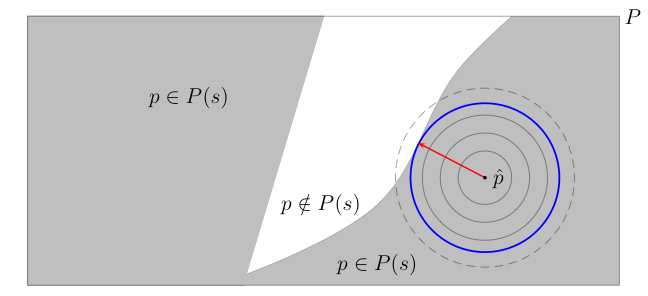
The picture is this:

Here $P$ denotes the set of values parameter $p$ can take, $P(s)$ denotes the set comprising of parameter values where the system is stable (shown in gray), and the white region represent the set of parameter values where the system is unstable. The radius of stability of the system at $\widetilde{p}$ is equal to the shortest distance from $\widetilde{p}$ to instability. It is the radius of the largest neighborhood around $\widetilde{p}$ all whose points are stable.

Clearly, this measure of robustness is inherently local in nature, as it explores the immediate neighborhood of the nominal value of the parameter, and the exploration is extended only as long as all the points in the extended neighborhood are stable. By design then, this measure does not attempt to explore the entire set of possible values of the parameter. Rather, it focuses on the immediate neighborhood of the nominal value of the parameter. The expansion of the neighborhood terminates as soon as an unstable value of the parameter is encountered. So technically, methods based on this measure of robustness, such as IGDT, are in fact based on a local worst-case analysis.

Note that under deep uncertainty the nominal value of the parameter can be substantially wrong, even just a wild guess. Furthermore, in this uncertain environment there is no guarantee that "true" value of the parameter is more likely to be in the neighborhood of the nominal value than in neighborhood of any other value of the parameter. That is, such a local analysis cannot be justified on the basis of "likelihood", or "plausibility", or "chance", or "belief" regarding the location of the true value of the parameter, simply because under deep uncertainty the quantification of the uncertainty is probability, likelihood, plausibility, chance, and belief FREE!.

In short, what emerges then is this:

IGDT's secret weapon for dealing with deep uncertainty: 
Ignore the severity of the uncertainty! Conduct a local analysis in the neighborhood of a poor estimate that may be substantially wrong, perhaps even just a wild guess. This magic recipe works particularly well in cases where the uncertainty is unbounded! 
The obvious flaws in the recipe should not bother you, and definitely should not prevent you from claiming that the method is reliable! To wit (color is used for emphasis):
The management of surprises is central to the “economic problem”, and info-gap theory is a response to this challenge. This book is about how to formulate and evaluate economic decisions under severe uncertainty. The book demonstrates, through numerous examples, the info-gap methodology for reliably managing uncertainty in economic policy analysis and decision making.
Ben-Haim (2010, p. x)

And I ask:

How can a methodology that ignores the severity of the uncertainty it is supposed to deal with possibly provide a reliable foundation for economic policy and decision making under such an uncertainty?

Despite the fact that the inherent local orientation of IGDT is well documented (at least since 2006), many publications continue to present IGDT as a theory for decision making under severe or deep uncertainty. The book under review is a typical example. So my question is this:

What is the rationale for the inclusion of two chapters dedicated to IGDT in a book whose goal is to provide the latest information on the state of the art in Decision-Making Under Deep Uncertainty?

One can add the following unavoidable, somewhat politically incorrect follow-up question:

How is it that the two IGDT chapters in the book somehow managed to be there without addressing at all the "local issue" and other well documented "critical issues" regarding the role and place of the theory in decision making under deep uncertainty?

For the record, it should be stressed that the "issues" with IGDT have been known (in public) at least since 2006. Here is a sample of quotes related to those "issues":

More recently, Info-Gap approaches that purport to be non-probabilistic in nature developed by Ben-Haim (2006) have been applied to flood risk management by Hall and Harvey (2009). Sniedovich (2007) is critical of such approaches as they adopt a single description of the future and assume alternative futures become increasingly unlikely as they diverge from this initial description. The method therefore assumes that the most likely future system state is known a priori. Given that the system state is subject to severe uncertainty, an approach that relies on this assumption as its basis appears paradoxical, and this is strongly questioned by Sniedovich (2007).
Bramley et al. (2009, 75 )

On the other hand, this simplicity of info-gap is also a weakness. On various occasions (e.g., Sniedovich (2008)), the info-gap approach has been criticized for relying on an inferential procedure on a specific estimate, generated from a specific model.
Sprenger (2011, p. 9)
Jan Sprenger (2011) The Precautionary Approach and the Role of Scientists in Environmental Decision-Making. Presented at the Philosophy of Science Association (PSA) 2010 Conference, November 4–6, 2010, Montréal, Quebec, Canada.

However, the critique by Sniedovich (2010), although often presented overly harsh, should be taken seriously.
Knoke (2011, p. 12)

Ecologists and managers contemplating the use of IGDT should carefully consider its strengths and weaknesses, reviewed here, and not turn to it as a default approach in situations of severe uncertainty, irrespective of how this term is defined. We identify four areas of concern for IGDT in practice: sensitivity to initial estimates, localized nature of the analysis, arbitrary error model parameterisation and the ad hoc introduction of notions of plausibility."
Hayes et al. (2013, p. 1)

Sniedovich (2008) bases his arguments on mathematical proofs that may not be accessible to many ecologists but the impact of his analysis is profound. It states that IGDT provides no protection against severe uncertainty and that the use of the method to provide this protection is therefore invalid.
Hayes et al. (2013, p. 2)

The literature and discussion presented in this paper demonstrate that the results of Ben-Haim (2006) are not uncontested. Mathematical work by Sniedovich (2008, 2010a) identifies significant limitations to the analysis. Our analysis highlights a number of other important practical problems that can arise. It is important that future applications of the technique do not simply claim that it deals with severe and unbounded uncertainty but provide logical arguments addressing why the technique would be expected to provide insightful solutions in their particular situation.
Hayes et al. (2013, p. 9)

Plausibility is being evoked within IGDT in an ad hoc manner, and it is incompatible with the theory's core premise, hence any subsequent claims about the wisdom of a particular analysis have no logical foundation. It is therefore difficult to see how they could survive significant scrutiny in real-world problems. In addition, cluttering the discussion of uncertainty analysis techniques with ad hoc methods should be resisted.
Hayes et al. (2013, p. 9)

Plausibility is being evoked within IGDT in an ad hoc manner, and it is incompatible with the theory's core premise, hence any subsequent claims about the wisdom of a particular analysis have no logical foundation. It is therefore difficult to see how they could survive significant scrutiny in real-world problems. In addition, cluttering the discussion of uncertainty analysis techniques with ad hoc methods should be resisted.
Hayes et al. (2013, p. 609)

Info-gap decision theory. Ben-Haim68,69 proposed info-gap decision theory as another way of dealing with cases where probabilities cannot be defined reliably. It has been used frequently to explore uncertainty in environmental management problems. Hayes et al.70 counted more than 20 info-gap studies in ecology. While use of info-gap decision theory has increased, so have criticisms. I have published papers using info-gap decision theory,71–74 but now I agree with critics that it overstates the level of uncertainty that it accommodates. Sniedovich75–78 is a vocal critic, although some turns of phrase (e.g., referring to "voodoo decision making") and his mathematical treatment might obscure the case in the eyes of many ecologists. Simultaneously, Sniedovich78 argues that defenders of info-gap do not address his major criticisms, which essentially dispute the form of uncertainty analyzed by info-gap decision theory.70
McCarthy (2014, pp. 87-88)

Satisficing-based robustness can further be subdivided into the concepts of global and local satisficing (Hall et al. 2012) (illustrated in Fig. 4). Global satisficing uses a measure similar to the domain criterion (Starr 1963). While the domain criterion quantifies the volume of the uncertainty space in which the decision maker’s performance requirements are met, the global satisficing metric measures the fraction of all plausible future scenarios (result of sampling the plausible ranges of each uncertain factor) that meet the requirements. The higher the fraction, the more robust an alternative is. Yet, a truly robust solution has to fulfill the performance requirements over all plausible future scenarios.In contrast, local satisficing does not take into account the whole uncertainty space but uses the concept of an uncertainty horizon to quantify robustness, an approach developed by Ben-Haim (2006). This approach is embedded in the Info-Gap which is further analyzed in the following section. The uncertainty horizon is the number of deviations from an uncertain parameter's best estimate that are allowed before the performance requirements are no longer fulfilled (Fig. 4). Local satisficing thus samples out-ward from a best estimate instead of sampling the whole uncertainty space which is basically the well-established concept of radius of stability (Sniedovich 2012). Local satisficing has been criticized as inadequate under deep uncertainty as under deep uncertainty, a best estimate cannot be made and is likely to prove very wrong (Sniedovich 2012).
Radke et a. (2017, p. 6 )

Criticism has been raised that Info-Gap, similar to RO, is not adequate for use under deep uncertainty as it uses local robustness (as described in Sect. 4) and therefore makes a best estimate of uncertain parameters (Sniedovich 2012).
Radke et a. (2017, p. 6 )

Its application under deep uncertainty, especially in Info-Gap, has therefore been criticized in the literature (Singh et al. 2015; Sniedovich 2012; Matrosov et al. 2013; Maier et al. 2016).
Radke et a. (2017, p. 13)

Summary and conclusions

It is a pity that the book missed a timely opportunity to clear the mess in the DMDU literature regarding the role and place of IGDT in the state of the art in decision making under deep uncertainty. The "DMDU Community" should be aware of the serious flaws in IGDT, and appreciate the reasons why this theory is not suitable for the treatment of deep uncertainty. Editors and referees of publications on Deep Uncertainty should assess IGDT for what it is, rather than for what the unsubstantiated rhetoric about it tells us.

Analysts and scholars who still believe that IGDT is suitable for the treatment of deep uncertainty should read carefully the review of Chapter 5.

There is a very simple, practical way for dealing with all the critical issues afflicting IGDT as a decision theory. All we have to do is accept the following inevitable conclusion.

DMDU's Axiom of Choice:
  • If your favorite uncertainty is DEEP, don't treat it with IGDT! 
  • If your favorite decision theory is IGDT, don't apply to your DEEP uncertainty. 
Warning! If you think that IGDT treats your uncertainty properly, then ... your beloved uncertainty is not DEEP, after all!

Bibliography and links

Articles/chapters

Research Reports

Links

Disclaimer: This site, its contents and style, are the responsibility of its owner the author and do not represent the views, policies or opinions of the organizations he is associated/affiliated with.